Парадокс спидометра. : Дискуссионные темы (Ф)

Ниже заготовка моего ответа по эой же теме на другой форум в ветку «Как назвать этот прибор». Но ответ не прошел, поскольку за минуту до его отправки я был забанен на месяц по понятным причинам. ———— Цитата: Цитата: Зачем же, — сделайте себе релятивистский трактор, и помечайте/измеряйте дорогу траками гусениц трактора/танка. Нижняя часть гусеницы относительно дороги не движется, то есть, копирует дорогу, не сокращается. Собственная скорость: Вот в том-то и проблема, вы предлагаете мне в это просто поверить.. Зачем же просто верить, Вы ведь человек разумный и можете проверить, по крайней мере, аналитически. Эту же тему я обсуждал еще на нескольких форумах и мой вывод из обсуждений следующий. Координатная скорость и собственная скорость являются равноправными физическими величинами, значения которых совпадают при малых скоростях. Используя любую из них, можно правильно описывать реально происходящие релятивистские движения, но математический формализм при использовании этих скоростей оказывается различным. Исследуя эти различия, мы можем понять причину нашумевших бурных споров о зависимости/независимости массы от скорости. Равноправие собственной и координатной скоростей сказывается не только на равноправии математических формализмов, но и идет значительно глубже: мы можем создать прибор/(систему приборов), который будет измерять либо координатную скорость, либо собственную скорость. Тогда возникает вопрос, а какую же скорость измеряет спидометр идеального релятивистского колесного автомобиля или идеального гусеничного танка. Анализ показывает, что ответ зависит от свойств, которые мы приписываем идеальному колесу / идеальной гусеничной ленте. Общие требования идеальности: пробуксовок с дорогой нет; мощность двигателя неограниченна; деформаций за счет центробежных сил нет. Требование по спидометру, измеряющему собственную скорость: В системе координат автомобиля движущийся обод колеса претерпевает точно такое же лоренцево сокращение, как и дорога. Следовательно, спицы колеса сжимаются под действием обода. В системе координат танка гусеничная лента претерпевает точно такое же лоренцево сокращение, как и дорога. Следовательно, балка с роликами А и Б на концах гусеницы сокращается под действием сокращающейся ленты. Требование по спидометру, измеряющему координатную скорость: В системе координат автомобиля спицы колеса претерпевают сокращение своей толщины, а их длина остается неизменной. Обод колеса не сокращается по законам СТО, а имеет тот же радиус, равный неизменной длине спиц. В системе координат танка движущаяся гусеничная лента не претерпевает никаких сокращений, поскольку она натянута на балку АБ, которая в системе танка не сокращается. Длина следов от траков такого танка будут тем длиннее, чем больше скорость танка. Пример: Пускай лента гусеницы имеет 20 башмаков. Тогда длина гусеничной балки равна 1, длина одного покоящегося башмака — 0.1. Если танк едет со скоростью 0,8c, то длина абсолютно упругой балки будет 0. 2)= 0,975609756… Гамма верхней части гусеницы: 4,555555555… Очевидно, на верхнюю часть гусеницы должно приходиться оставшиеся 16,4 башмака, длиной 0,1 каждый. Разделив 1,64 на 4,55555… получаем 0,36, то есть, длину балки гусеницы танка в системе дороги. Поэтому проблем нет. С одним шипом гусеницы связываем зуб перемыкающий два контакта после каждого полного оборота гусеничной ленты танка, измеряя таким образом истинную длину дороги. Делим эту величину на количество тик-так часов в танке, и получаем собственную скорость танка, предел которой равен бесконечности. Если же мы сооружаем танк со спидометром, измеряющим координатную скорость, то балка гусеницы должна быть абсолютно упругой, а гусеничная лента растягивается на ней тем больше, чем больше скорость танка. Растяжение следов башмаков такой гусеничной ленты на дороге во столько же раз больше от следов покоящегося танка, во столько раз собственное время между событиями 1 и 2 меньше координатного времени между этими событиями. Лично мне танк, оставляющий после себя следы разной длины, в зависимости от скорости, кажется не совсем идеальным. Поэтому мне больше импонирует танк оставляющий эталонные следы и измеряющий собственную скорость. Кроме того, наш внутренний спидометр измеряет собственную скорость. Её же измеряет и спидометр с торчащими контактами, замыкающимися на километровых столбах. Но ничего не попишешь, — дуализм и равноправие математических формализмов идут в область практического описания. PS: Где-то я слышал, что формализм собственной скорости развивал Ричард Фейнман, но то ли не доделал, то ли было некогда.. PS2: Квантуемая скорость значительно более обещающая, но за этим БАКом все некогда ей уделить должное внимание. «Пристегните ремни – Будем размножаться!»

Физические величины. Измерение физических величин » Народна Освіта

Как вы думаете, насколько часто люди выполняют измерения? Насколько важно уметь делать это правильно? Каких последствий следует ожидать, если результаты измерений будут ошибочными? Чтобы помочь вам ответить на эти вопросы, напомним несколько приборов, которыми вы и ваша семья пользуетесь практически ежедневно: часы, весы, термометр, спидометр, манометр. .. Надеемся, вы убедились в необходимости внимательно изучить этот параграф!

 

определяем понятие «физическая величина»

Для описания каких-либо явлений или свойств тел люди издавна используют их характеристики. Например, когда мы говорим, что теннисный шарик меньше воздушного шара, то имеем в виду, что объем теннисного шарика меньше объема воздушного шара. Объем — пример физической величины. Эта величина характеризует общее свойство тел занимать некоторую часть пространства (рис. 4.1, а). Еще одним примером физической величины может служить уже известное вам понятие скорость движения, которое является характеристикой движения тел (рис. 4.1, б).

Физическая величина — это количественно выраженная характеристика тела или физического явления.

Разумеется, объем и скорость движения — это далеко не все физические величины, которыми оперирует физика. Даже в повседневной жизни мы имеем дело с большим количеством физических величин: длина, площадь, объем, масса, время, путь, температура.

Какую физическую величину измеряет человек при простуде?

Для удобства каждую физическую величину обозначают определенным символом (буквой латинского или греческого алфавита). Например, объем обозначают символом V, время — символом t, скорость движения — символом и.

узнаем о Международной системе единиц

В романе Жюля Верна «Пятнадцатилетний капитан» есть такой эпизод: «Пройдя шагов триста по берегу реки, маленький отряд вступил под покров девственного леса, по извилистым тропинкам которого ему предстояло странствовать…»

Проанализируем этот отрывок и выясним, какую физическую величину имел в виду автор, чему равно ее числовое значение и в каких единицах была измерена эта величина. Нетрудно установить, что речь идет о физической величине путь; числовое значение этой физической величины — триста; единицей пути служит один шаг.

Очевидно, что в большинстве случаев выбор шага как единицы пути не может быть удачным, ведь длина шага у всех разная (рис. 4.2). Таким образом, становится понятным, почему люди с древних времен начали договариваться о том, чтобы измерять одну и ту же физическую величину одинаковыми единицами.

Сейчас в большинстве стран мира действует введенная в 1960 г. Международная система единиц, которую называют Система Интернациональная (СИ) (рис. 4.3).

В СИ единицей длины является метр (м), единицей времени — секунда (с), объем измеряется в метрах кубических (м³), скорость движения — в метрах в секунду (м/с). О других единицах СИ вы узнаете позже.

При записи значения физической величины указывают символ, которым она обозначается, числовое значение физической величины и ее единицу. Например, запись V = 5 м/с означает, что скорость движения некоего тела составляет 5 метров в секунду.

выясняем, чем кратные единицы отличаются от дольных

Для удобства записи больших и малых значений физических величин используют кратные и дольные единицы.

Кратные единицы — это единицы, которые больше основных единиц в 10, 100, 1000 и более раз.

Дольные единицы — это единицы, которые меньше основных единиц в 10, 100, 1000 и более раз.

Названия кратных и дольных единиц включают в себя специальные префиксы. Например, километр (1000 м) — кратная единица длины; сантиметр (0,01 м) — дольная единица длины.

В таблице на с. 27 приведены наиболее часто употребляемые префиксы.

Префиксы для образования названий кратных и дольных единиц

выясняем, чем отличаются прямые и косвенные измерения

Значения физических величин получают путем измерений.

Вспомните пример измерения, приведенный в п. 2 этого параграфа. Автор, описывая путешествие отряда по берегу реки, в качестве единицы пути выбрал шаг. Чтобы выразить числовое значение (триста) пути в шагах, ему необходимо было сравнить пройденное расстояние с длиной шага.

измерить физическую величину означает сравнить ее с однородной величиной, взятой за единицу.

Существует два вида измерений: прямые и косвенные измерения.

При прямом измерении искомое значение физической величины получают сразу — по показаниям измерительного прибора (рис. 4.4, 4.5).

При косвенном измерении искомое значение физической величины определяют с помощью формулы, подставив в нее значения других физических величин, полученных в ходе прямых измерений. Так, чтобы определить площадь 5 прямоугольника, сначала с помощью линейки измеряют длину I и ширину d прямоугольника (прямые измерения), а потом вычисляют его площадь по формуле 5 = I ■ d.

Косвенные измерения каких величин вы выполняли на уроках математики?

знакомимся с измерительными приборами

Для установления значений физических величин в ходе прямых измерений используют измерительные приборы (рис. 4.6).

Сейчас в науке, технике, быту применяют как электронные цифровые измерительные приборы, у которых значение измеряемой величины высвечивается на экране, так и измерительные приборы, при пользовании которыми значение измеряемой величины определяют по шкале. Измерительный прибор обычно содержит информацию о единицах, в которых поданы значения измеряемой этим прибором величины.

По шкале можно установить две самые важные характеристики измерительного прибора: цену деления шкалы прибора и пределы измерения*.

Цена деления шкалы измерительного прибора — это значение наименьшего деления шкалы данного прибора.

Чтобы определить цену деления шкалы измерительного прибора, необходимо разность двух любых ближайших значений величины, приведенных на шкале, разделить на количество делений между ними.

Пределы измерения электронных цифровых приборов определяют по его паспорту. Существуют приборы, пределы измерения которых устанавливают специальным переключателем.

 

Определим цену деления шкалы медицинского термометра (рис. 4.7):

1) выберем два любых значения температуры, которые обозначены на шкале и стоят рядом, например 40 °С и 39 °С, и найдем их разность: 40 °С — 39 °С = 1 °С;

2) определим количество делений между метками, рядом с которыми указаны данные значения, — 10 делений;

3) полученную разность разделим на количество делений:

 

 

Итак, цена деления шкалы данного термометра составляет 0,1 ^

 

Пределы измерения прибора — это наибольшее и наименьшее значения физической величины, которые можно измерить этим прибором.

Так, верхний предел измерений медицинского термометра на рис. 4.7 равен 42 °С, нижний предел составляет 34,1 °С.

.Подводим итоги

Физическая величина — это количественно выраженная характеристика тела или физического явления. Измерить физическую величину — значит сравнить ее с однородной величиной, взятой за единицу.

Записывая значение физической величины, следует привести символ, которым она обозначается, числовое значение физической величины и ее единицу. Для удобства записи больших и малых значений физических величин используют кратные и дольные единицы — их названия содержат специальные префиксы.

Цена деления шкалы измерительного прибора — это значение наименьшего деления шкалы этого прибора. Пределы измерения прибора — это наибольшее и наименьшее значения физической величины, которые можно измерить данным прибором.

Контрольные вопросы

1. Дайте определение физической величины. 2. Приведите примеры физических величин. Какие свойства тел или какие признаки физических явлений они характеризуют? 3. Какими символами обозначают объем; скорость движения; время движения тела? 4. Что значит измерить физическую величину? 5. Приведите примеры префиксов, используемых в названиях дольных единиц; кратных единиц. 6. Приведите примеры измерительных приборов. 7. Какие характеристики прибора можно выяснить с помощью его шкалы? 8. Что такое цена деления шкалы прибора?

 

Упражнение № 4

1. Представьте в метрах значения физических величин: 145 мм; 1,5 км; 2 км 32 м.

2. Назовите физические величины, приборы для измерения которых изображены на рис. 1-3. Укажите символы для обозначения этих величин; их единицы в СИ.

4. Запишите, используя кратные или дольные единицы: 0,000 007 5 м — диаметр красных кровяных телец; 5 900 000 000 000 м — радиус орбиты карликовой планеты Плутона; 6 400 000 м — радиус Земли.

5. Баскетбольная площадка, на которой проходят официальные соревнования, должна иметь длину 28 м и ширину 15 м. Определите площадь баскетбольной площадки. Ответ запишите также в дм² и см².

6. Вспомните определение физической величины и докажите, что длина — это физическая величина.

7. Воспользуйтесь дополнительными источниками информации и подготовьте сообщение об измерительных приборах, с которыми вы имеете дело в повседневной жизни.

Экспериментальные задания

1. Найдите у себя дома 2-3 измерительных прибора, имеющих шкалу.

Определите пределы измерения и цену деления шкалы каждого прибора.

 

2. Воспользовавшись приведенной ниже информацией, выясните площадь вашей ладони. Площадь фигуры, имеющей неправильную геометрическую форму, можно определить по контуру этой фигуры, нарисованному на бумаге в клетку, или с помощью палетки — прозрачной пластинки с нанесенной на ней сеткой квадратов определенной площади. В таких случаях площадь в фигуры вычисляют по формуле:

где п — количество целых квадратов; Ъ — количество нецелых квадратов; в₀ — площадь одного квадрата. Таким образом, площадь фигуры на рисунке равна:

 

3. В свое время древнегреческий математик, физик и механик Архимед предложил способ измерения площади фигуры, имеющей неправильную геометрическую форму, с помощью точных весов. Попробуйте воспроизвести этот способ и объяснить его.

Физика и техника в Украине

Национальная академия наук Украины

(НАНУ) — высшая государственная научная организация Украины. Основана в 1918 г. правительством гетмана П. П. Скоропадско-го. Первым президентом Украинской академии наук (такое название носила НАНУ в то время) был выдающийся украинский ученый Владимир Иванович Вернадский.

НАНУ занимается исследованиями в области естественных, гуманитарных, общественных и технических наук.

Крупнейшие достижения Академии: осуществление искусственной ядерной реакции превращения ядер Лития в ядра Гелия; создание ускорителя заряженных частиц, радиолокатора нового типа; внедрение технологии автоматической сварки; создание новых лекарственных препаратов и методов лечения; разработка первой в континентальной Европе электронной вычислительной машины (ЭВМ). В разное время в НАНУ работали многие выдающиеся ученые, сформировалось множество научных школ. Так, во всем мире известны украинские школы электросварки Е. О. Патона и Б. Е. Патона, кибернетики С. А. Лебедева и В. М. Глушкова, теоретической физики Л. Д. Ландау, нелинейной механики и статистической физики Н. Н. Боголюбова и др.

 

лабораторная работа № 1

тема. определение цены деления шкалы измерительного прибора.

Цель: определить пределы измерения и цену деления шкалы каждого из предложенных измерительных приборов.

оборудование: линейка; термометр; другие измерительные приборы.

указания к работе

подготовка к эксперименту

Убедитесь, что вы знаете ответы на следующие вопросы.

1) Что называют измерительным прибором?

2) Как определить пределы измерения прибора?

3) Как определить цену деления шкалы прибора?

4) Какие правила безопасности следует соблюдать, работая с термометром?

Эксперимент

Строго придерживайтесь инструкции по безопасности (см. форзац).

1. Рассмотрите шкалы имеющихся у вас измерительных приборов.

2. Заполните первые пять столбцов таблицы.

обработка результатов эксперимента

Определите цену деления шкалы и пределы измерения каждого из исследуемых приборов и закончите заполнение таблицы.

Анализ эксперимента и его результатов

Сформулируйте вывод, в котором укажите: 1) что именно вы определяли; 2) какие результаты получили; 3) для чего могут понадобиться умения, приобретенные в ходе выполнения работы.

творческое задание

Изготовьте мерную ленту с ценой деления шкалы 5 мм.

 

Это материал учебника Физика 7 класс Барьяхтар, Довгий

 

Спидометр автомобиля измеряет скорость или скорость? Объяснять.

Literature guidesConcept explainersWriting guidePopular textbooksPopular high school textbooksPopular Q&ABusinessAccountingEconomicsFinanceLeadershipManagementMarketingOperations ManagementEngineeringBioengineeringChemical EngineeringCivil EngineeringComputer EngineeringComputer ScienceElectrical EngineeringMechanical EngineeringLanguageSpanishMathAdvanced MathAlgebraCalculusGeometryProbabilityStatisticsTrigonometryScienceAdvanced PhysicsAnatomy and PhysiologyBiochemistryBiologyChemistryEarth ScienceHealth & NutritionNursingPhysicsSocial ScienceAnthropologyGeographyHistoryPolitical SciencePsychologySociology

learn

write

plus

Log In

University Physics with Modern Physics (14th Edition)

14th Edition

ISBN: 9780321973610

Author: Hugh D. Young, Roger A. Freedman

Publisher: PEARSON

Не помогает? См. похожие книги

Университетская физика с современной физикой (14-е издание)

Движение по прямой. 2.1DQ

Глава 2, Задача 2.1DQ

Спидометр автомобиля измеряет скорость или скорость? Объяснять.

Спидометр автомобиля измеряет скорость или скорость.

Спидометр не измеряет направление автомобиля это означает, что спидометр не измеряет скорость автомобиля. Следовательно, спидометр измеряет скорость автомобиля.

Скорость определяется как отношение расстояния, пройденного частицей, ко времени, затраченному частицей. Скорость является скалярной величиной.

Скорость определяется как отношение смещения частицы ко времени, затраченному частицей. Скорость является векторной величиной, и направление скорости совпадает с направлением перемещения.

Вывод:

Спидометр не измеряет направление движения автомобиля, это означает, что спидометр не измеряет скорость автомобиля. Следовательно, спидометр измеряет скорость автомобиля.

Хотите увидеть больше полных решений, подобных этому?

Подпишитесь сейчас, чтобы получить доступ к пошаговым решениям миллионов задач из учебников, написанных экспертами в данной области!

расписание 00:53

chevron_left

Предыдущий CHEVRON_LEFT

ГЛАВА 2.5, задача 2.5TYU

CHEVRON_RINGE

Следующая CHEVRON_RIGHT

Глава 2, задача 2.2DQ

делает спиртометр CAR SEARP OR VELOCITY?

Автомобильный спидометр измеряет скорость, скорость или и то, и другое? Объясните

Что автомобильный спидометр измеряет скорость или скорость? Объяснять.

Университетская физика с современной физикой (14-е издание)

14-е издание

ISBN: 9780321973610

Автор: Хью Д. Янг, Роджер А. Фридман

Издатель: PEARSON

Бесполезно? См. похожие книги

Университетская физика с современной физикой (14-е издание)

Движение по прямой. 2.1DQ

Время, скорость и скорость | Физика

Цели обучения

К концу этого раздела вы сможете:

• Объяснять отношения между мгновенной скоростью, средней скоростью, мгновенной скоростью, средней скоростью, перемещением и временем.
• Вычислить скорость и скорость, зная начальное положение, начальное время, конечное положение и конечное время.
• Построить график зависимости скорости от времени по графику зависимости положения от времени.
• Интерпретация графика зависимости скорости от времени.

Рисунок 1. Движение этих мчащихся улиток можно описать их скоростями и скоростями. (кредит: tobitasflickr, Flickr)

Движение — это нечто большее, чем расстояние и смещение. Такие вопросы, как «Сколько времени занимает пеший забег?» и «Какова была скорость бегуна?» нельзя ответить без понимания других понятий. В этом разделе мы добавляем определения времени, скорости и скорости, чтобы расширить наше описание движения.

Как обсуждалось в разделе Физические величины и единицы измерения, наиболее фундаментальные физические величины определяются тем, как они измеряются. Так обстоит дело со временем. Каждое измерение времени связано с измерением изменения некоторой физической величины. Это может быть цифра на цифровых часах, сердцебиение или положение Солнца на небе. В физике время определяется просто:

время равно изменению или интервалу, в течение которого происходит изменение. Невозможно узнать, что время прошло, если что-то не изменится.

Количество времени или изменения калибруется путем сравнения со стандартом. Единицей времени в СИ является секунда, сокращенно с. Мы могли бы, например, заметить, что некий маятник совершает полный оборот каждые 0,75 с. Затем мы могли бы использовать маятник для измерения времени, считая его колебания или, конечно же, подключив маятник к часовому механизму, который регистрирует время на циферблате. Это позволяет нам не только измерять количество времени, но и определять последовательность событий.

Как время связано с движением? Обычно нас интересует время, затраченное на определенное движение, например, сколько времени требуется пассажиру самолета, чтобы добраться от своего места до задней части самолета. Чтобы найти прошедшее время, мы отмечаем время в начале и в конце движения и вычитаем два. Например, лекция может начаться в 11:00. и закончить в 11:50, так что прошедшее время будет 50 мин.

Elapsed time Δ t is the difference between the ending time and beginning time,

Δ t  =  t _f  −  t ₀ ,

where Δ t is изменение во времени или прошедшее время, t _f — время в конце движения, а t ₀ — время в начале движения. (Как обычно, дельта-символ Δ означает изменение величины, следующей за ним.)

Жизнь проще, если время начала t ₀ принять за ноль, как при использовании секундомера. Если бы мы использовали секундомер, он просто показывал бы ноль в начале лекции и 50 минут в конце. Если

t ₀ = 0, то Δ t = t _f ≡ t .

В этом тексте для простоты

• начало движения в момент времени, равный нулю ( t ₀ = 0)
• символ t используется для обозначения прошедшего времени, если не указано иное (Δ t = t _f ≡ t )

Скорость

Ваше понятие скорости, вероятно, совпадает с ее научным определением. Вы знаете, что если у вас есть большое перемещение за небольшой промежуток времени, у вас будет большая скорость, и эта скорость имеет единицы измерения расстояния, деленные на время, такие как мили в час или километры в час.

Средняя скорость

Средняя скорость равна смещению (изменению положения), деленному на время в пути ,

[латекс]\bar{v}=\frac{\Delta x}{\Delta t}= \frac{{x}_{f}-{x}_{0}}{{t}_{f}-{t}_{0}}\\[/latex],

, где[латекс]\ bar{v}\\[/latex] — средняя (обозначенная чертой над v ) скорость , Δ x — изменение положения (или смещения) и x _f и х ₀ — конечная и начальная позиции в моменты времени t _f и t ₀ соответственно. Если начальное время t ₀ принято равным нулю, то средняя скорость равна просто

[латекс]\бар{в}=\фракция{\Дельта х}{т}\\[/латекс].

Обратите внимание, что это определение указывает, что скорость является вектором, потому что смещение является вектором . Она имеет как величину, так и направление. Единицей скорости в СИ является метр в секунду или м/с, но широко используются многие другие единицы, такие как км/ч, мили/ч (также пишется как миль/ч) и см/с. Предположим, например, что пассажиру самолета потребовалось 5 секунд, чтобы переместиться на -4 м (знак минус указывает, что перемещение происходит в направлении задней части самолета). Его средняя скорость была бы

[латекс]\bar{v}=\frac{\Delta x}{t}=\frac{-4\text{m}}{5\text{s}}=-\text{0,8 м/с .}\\[/latex]

Знак минус указывает, что средняя скорость также направлена ​​к задней части самолета.

Однако средняя скорость объекта ничего не говорит нам о том, что происходит с ним между начальной и конечной точками. Например, по средней скорости мы не можем сказать, остановился ли пассажир самолета на мгновение или дал задний ход перед тем, как подойти к задней части самолета. Чтобы получить больше деталей, мы должны рассмотреть меньшие отрезки пути за меньшие промежутки времени.

Рис. 2. Более подробная запись пассажира самолета, направляющегося к задней части самолета, показывающая небольшие сегменты его поездки.

Чем меньше временных интервалов, учитываемых в движении, тем детальнее информация. Когда мы доводим этот процесс до его логического завершения, остается бесконечно малый интервал. За такой интервал средняя скорость становится мгновенной скоростью или скоростью в конкретный момент . Автомобильный спидометр, например, показывает величину (но не направление) мгновенной скорости автомобиля. (Полиция выписывает штрафы на основе мгновенной скорости, но при расчете времени, которое потребуется, чтобы добраться из одного места в другое во время дорожного путешествия, вам необходимо использовать среднюю скорость. ) Мгновенная скорость v — средняя скорость в конкретный момент времени (или за бесконечно малый интервал времени).

Математически нахождение мгновенной скорости v в точный момент времени t может потребовать ограничения, вычислительной операции, выходящей за рамки этого текста. Однако во многих случаях мы можем найти точные значения мгновенной скорости без вычислений.

В повседневном языке большинство людей используют термины «скорость» и «скорость» как синонимы. Однако в физике они не имеют одинакового значения и представляют собой разные понятия. Одним из основных отличий является то, что скорость не имеет направления. Таким образом скорость является скаляром . Точно так же, как нам нужно различать мгновенную скорость и среднюю скорость, нам также необходимо различать мгновенную скорость и среднюю скорость.

Мгновенная скорость — величина мгновенной скорости. Например, предположим, что пассажир самолета в какой-то момент имел мгновенную скорость -3,0 м/с (минус означает по направлению к задней части самолета). При этом его мгновенная скорость была 3,0 м/с. Или предположим, что в какой-то момент во время похода по магазинам ваша мгновенная скорость составляет 40 км/ч строго на север. Ваша мгновенная скорость в этот момент будет 40 км/ч — та же величина, но без указания направления. Однако средняя скорость сильно отличается от средней скорости. Средняя скорость — это пройденное расстояние, деленное на прошедшее время.

Мы заметили, что пройденное расстояние может быть больше, чем перемещение. Таким образом, средняя скорость может быть больше, чем средняя скорость, которая равна смещению, деленному на время. Например, если вы едете в магазин и через полчаса возвращаетесь домой, а одометр вашего автомобиля показывает, что общее пройденное расстояние составило 6 км, то ваша средняя скорость составила 12 км/ч. Однако ваша средняя скорость была равна нулю, потому что ваше смещение за кругосветное путешествие равно нулю. (Перемещение — это изменение положения и, таким образом, равно нулю для кругового рейса. ) Таким образом, средняя скорость равна не просто величина средней скорости.

Рисунок 3. За 30 минут пути туда и обратно до магазина общее пройденное расстояние составляет 6 км. Средняя скорость 12 км/ч. Перемещение для кругового рейса равно нулю, так как нет чистого изменения положения. Таким образом, средняя скорость равна нулю.

Другой способ визуализации движения объекта — использование графика. График зависимости положения или скорости от времени может быть очень полезен. Например, для этой поездки в магазин графики положения, скорости и зависимости скорости от времени показаны на рис. 4. (Обратите внимание, что эти графики изображают очень упрощенную модель поездки. Мы предполагаем, что скорость постоянна во время поездки, что нереально, учитывая, что мы, вероятно, остановимся у магазина. Но для простоты мы будем моделировать его без остановок или изменения скорости. Мы также предполагаем, что маршрут между магазином и домом — совершенно прямая линия. )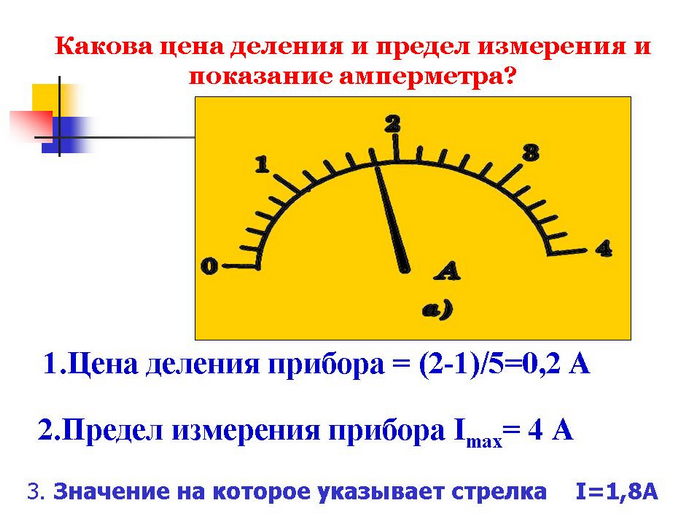

Рисунок 4. Положение относительно времени, скорость относительно времени и скорость относительно времени в пути. Обратите внимание, что скорость обратного пути отрицательна.

Установление связей: домашнее расследование — ощущение скорости

Если вы провели много времени за рулем, вы, вероятно, хорошо чувствуете скорость от 10 до 70 миль в час. Но что это в метрах в секунду? Что мы имеем в виду, когда говорим, что что-то движется со скоростью 10 м/с? Чтобы лучше понять, что на самом деле означают эти значения, сделайте несколько наблюдений и расчетов самостоятельно:

• рассчитайте типичную скорость автомобиля в метрах в секунду
• оцените скорость бега трусцой и ходьбы, самостоятельно измеряя время; конвертировать измерения как в м/с, так и в мили/ч
• определить скорость муравья, улитки или падающего листа

Проверьте свое понимание

Пригородный поезд идет из Балтимора в Вашингтон, округ Колумбия, и обратно за 1 час 45 минут. Расстояние между двумя станциями составляет примерно 40 миль. Чему равна а) средняя скорость поезда и б) средняя скорость поезда в м/с?

Решение

(a) Средняя скорость поезда равна нулю, потому что x _f  = x ₀ ; поезд останавливается там же, где и стартовал.

(b) Средняя скорость поезда рассчитывается ниже. Обратите внимание, что поезд проезжает 40 миль в одну сторону и 40 миль обратно, а общее расстояние составляет 80 миль.

[латекс]\frac{\text{расстояние}}{\text{время}}=\frac{\text{80 миль}}{\text{105 минут}}\\[/латекс]

[латекс ] \ frac {\ text {80 миль}} {\ text {105 минут}} \ times \ frac {\ text {5280 футов}} {\ text {1 миля}} \ times \ frac {\ text {1 метр} }{3\text{.}\text{28 футов}}\times \frac{\text{1 минута}}{\text{60 секунд}}=\text{20 м/с}\\[/latex]

Резюме раздела

• Время измеряется с точки зрения изменения, и его единицей СИ является секунда (с). В исходном времени для события состоит Δ T = T _F — T ₀ , где T _F — это окончательное время, и T _{01388. Начальное время часто принимается равным нулю, как если бы оно измерялось секундомером; тогда прошедшее время составляет всего t .}
• Средняя скорость [латекс]\бар{в}\\[/латекс] определяется как смещение, деленное на время в пути. В символах средняя скорость

  [латекс]\stackrel{-}{v}=\frac{\Delta x}{\Delta t}=\frac{{x}_{\text{f}}-{x}_{0}}{ {t}_{\text{f}}-{t}_{0}}\\[/латекс].

• Единицей скорости в системе СИ является м/с.
• Скорость является вектором и поэтому имеет направление.
• Мгновенная скорость v — это скорость в конкретный момент времени или средняя скорость за бесконечно малый интервал.
• Мгновенная скорость — это величина мгновенной скорости.
• Мгновенная скорость является скалярной величиной, поскольку для нее не указано направление.
• Средняя скорость равна общему пройденному расстоянию, деленному на прошедшее время. (Средняя скорость равна , а не величине средней скорости.) Скорость — это скалярная величина; с ним не связано никакого направления.

Концептуальные вопросы

1. Приведите пример (но не из текста) устройства, используемого для измерения времени, и определите, какое изменение в этом устройстве указывает на изменение времени.

2. Существует различие между средней скоростью и величиной средней скорости. Приведите пример, иллюстрирующий разницу между этими двумя величинами.

3. Одометр автомобиля измеряет положение или перемещение? Его спидометр измеряет скорость или скорость?

4. Если вы делите общее расстояние, пройденное за поездку на автомобиле (определяемое одометром), на время в пути, вы рассчитываете среднюю скорость или величину средней скорости? При каких обстоятельствах эти две величины совпадают?

5. Как связаны между собой мгновенная скорость и мгновенная скорость? Чем они отличаются?

Задачи и упражнения

1. (a) Рассчитайте среднюю скорость Земли относительно Солнца. б) Какова его средняя скорость за период в один год?

2. Лопасть вертолета вращается со скоростью ровно 100 оборотов в минуту. Его оконечность находится в 5,00 м от центра вращения. (a) Рассчитайте среднюю скорость кончика лопасти в системе отсчета вертолета. б) Какова его средняя скорость за один оборот?

3. Североамериканский и Европейский континенты раздвигаются со скоростью около 3 см/год. При такой скорости за какое время они разлетятся на 500 км дальше, чем в настоящее время?

4. Земля к западу от разлома Сан-Андреас в южной Калифорнии движется со средней скоростью около 6 см/год на северо-запад относительно земли к востоку от разлома. Лос-Анджелес находится к западу от разлома и, таким образом, когда-нибудь может оказаться на той же широте, что и Сан-Франциско, который находится к востоку от разлома. Как далеко в будущем это произойдет, если смещение должно быть сделано на 590 км к северо-западу, если предположить, что движение остается постоянным?

5. 26 мая 1934 года обтекаемый дизельный поезд из нержавеющей стали под названием «Зефир» установил мировой рекорд скорости для поездов дальнего следования без остановок. Его пробег из Денвера в Чикаго занял 13 часов 4 минуты 58 секунд, и его видели более миллиона человек на маршруте. Общее пройденное расстояние составило 1633,8 км. Какова его средняя скорость в км/ч и м/с?

6. Приливное трение замедляет вращение Земли. В результате орбита Луны увеличивается в радиусе со скоростью примерно 4 см/год. Если предположить, что это постоянная скорость, сколько лет пройдет, прежде чем радиус орбиты Луны увеличится на 3,84 × 10 ⁶ м (1%)?

7. Студентка ехала в университет из своего дома и отметила, что показания одометра ее автомобиля увеличились на 12,0 км. Поездка заняла 18,0 мин. а) Какова была ее средняя скорость? (b) Если расстояние по прямой от ее дома до университета составляет 10,3 км в направлении 25,0° к югу от востока, какова была ее средняя скорость? в) Если она вернулась домой тем же путем через 7 ч 30 мин после того, как уехала, каковы были ее средняя скорость и скорость за весь путь?

8. Скорость распространения потенциала действия (электрического сигнала) в нервной клетке зависит (обратно) от диаметра аксона (нервного волокна). Если нервная клетка, соединяющая спинной мозг с вашими ногами, имеет длину 1,1 м, а скорость нервного импульса составляет 18 м/с, сколько времени потребуется нервному сигналу, чтобы пройти это расстояние?

9. Разговоры с космонавтами на лунной поверхности характеризовались своеобразным эхом, при котором голос находящегося на земле человека был настолько громким в космическом шлеме космонавта, что улавливался микрофоном космонавта и передавался обратно на Землю. Разумно предположить, что время эха равно времени, необходимому для прохождения радиоволны от Земли до Луны и обратно (то есть без учета временных задержек в электронном оборудовании). Рассчитайте расстояние от Земли до Луны, учитывая, что время отражения составляет 2,56 с и что радиоволны распространяются со скоростью света (3,00 × 10 ⁸ м/с).

10. Футбольный защитник пробегает 15,0 м прямо по игровому полю за 2,50 с. Затем его ударили и толкнули на 3,00 м прямо назад за 1,75 с. Он прерывает захват и бежит вперед еще 21,0 м за 5,20 с. Вычислите его среднюю скорость (а) для каждого из трех интервалов и (б) для всего движения.

11. Планетарная модель атома изображает электроны, вращающиеся вокруг ядра атома так же, как планеты вращаются вокруг Солнца. В этой модели вы можете рассматривать водород, простейший атом, с одним электроном на круговой орбите 1,06 × 10 ^-10 м в диаметре. а) Если известно, что средняя скорость электрона на этой орбите равна 2,20 × 10 90 403 6 90 404 м/с, вычислите число оборотов, которое он совершает вокруг ядра в секунду. б) Какова средняя скорость электрона?

Глоссарий

средняя скорость:

пройденное расстояние, деленное на время, в течение которого происходит движение

средняя скорость:

смещение разделить на время, в течение которого происходит смещение

мгновенная скорость:

скорость в конкретный момент или средняя скорость за бесконечно малый интервал времени

мгновенная скорость:

величина мгновенной скорости

время:

изменение или интервал, в течение которого происходит изменение

Модель:

упрощенное описание, содержащее только те элементы, которые необходимы для описания физики физической ситуации

истекшее время:

разница между временем окончания и временем начала

Выбранные решения для упражнений и задач

1.