Максимальный вращающий магнитный момент | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Загрузка…

Рис. 6.8. Вращающее действие маг­нитного поля на виток с током

Действие магнитного поля на виток с током позволяет использовать его и для определения модуля магнитной индукции. По­ворачивание витка в магнитном поле свиде­тельствует о том, что на него действуют по меньшей мере две силы. Равнодействующие этих сил будут приложены в точках A и B (рис. 6.8). Вращающий момент, действую­щий на виток, будет равен произведению одной из этих сил F̅ на радиус витка r. Этот момент не обязательно рассчитывать. Его можно измерить с помощью спиральной пружины или другого чувствительного ус­тройства для измерения механического мо­мента, соединенных с витком.

Опыты показывают, что виток с током в магнитном поле всегда поворачивается так, что направление его нормали n̅ совпадает с направлением магнитной индукции исследуемого поля

B̅. Очевидно, что в этом случае вращающий момент будет равен нулю. Он будет иметь максимальное значение тогда, когда угол между магнитной индукцией B̅ и нормалью n̅ будет равен 90°.

Магнитную индукцию можно определить по силовому дей­ствию магнитного поля на ви­ток с током.

Загрузка…

Не изменяя силы тока в проводнике, исследуем, как зависит значение максималь­ного вращающего момента от параметров витка.

Расположив виток на определенном рас­стоянии от проводника с током, измерим максимальный вращающий момент M_max для определенного значения силы тока в витке I₁. Увеличим силу тока в витке в два раза. При I₂ = 2I₁ максимальный ме­ханический момент будет равен M_max

2 = 2M_max1. То же самое будем наблюдать при увеличении силы тока в 3, 4, 5 раз. Таким образом, максимальное значение вращающего момента, который действует на виток с током, будет пропорциональным силе тока в витке

M_max ~ I_вит.

Вращающий момент, дейст­вующий на виток в магнитном поле, пропорционален силе то­ка в нем. Материал с сайта http://worldofschool.ru

Если заменить данный виток другим, с большей или меньшей площадью S_вит, то заметим соответствующее увеличение или уменьшение значения максимального вращающего момента. Таким образом,

макси­мальный вращающий момент, который дей­ствует на виток в магнитном поле, пропор­ционален его площади:

M_max ~ S_вит.

Объединив результаты обоих этапов ис­следования, получим

M_max ~ I_вит • S_вит.

На этой странице материал по темам:

• Чему равен максимальный вращающий момент сил действующих 100 витков

• Разница между максимальным вращающим моментом физика

• Максимальный вращающий

• Максимальный вращающий момент формула физика

• Определить вращающий момент, действующий на виток

Материал с сайта http://WorldOfSchool.ru

что такое, формула и в чем измеряется

Мощность двигателя – важнейший его показатель. Как в плане эксплуатации, так и в плане начисления налогов на авто. Крутящий момент нередко путают с мощностью или упускают его из виду в процессе оценки ходовых качеств авто. Многие упрощают автомобиль, считая, что большое количество лошадиных сил – главное преимущество любого мотора. Однако, вращающий момент – более важный показатель. Особенно, если автомобиль не предполагается использовать в качестве спортивного.

Содержание

1. Что такое крутящий момент
2. Формула расчета крутящего момента
3. От чего зависит крутящий момент
4. На что влияет крутящий момент
5. Как увеличить крутящий момент
6. Определение крутящего момента на валу
7. Измеритель крутящего момента
8. Датчик крутящего момента
9. Максимальный крутящий момент
10. Какому двигателю отдать предпочтение
11. Бензиновый двигатель
12. Дизельный двигатель
13. Электродвигатель
14. Улучшение разгона авто за счет изменения момента вращения
15. Зависимость мощности от крутящего момента

Что такое крутящий момент

Крутящим моментом называют единицу силы, которая необходима для поворота коленчатого вала ДВС. Эта не «лошадиная сила», которой должна обозначаться мощность.

ДВС вырабатывает кинетическую энергию, вращая таким образом коленвал. Показатель мощности двигателя (сила давления) зависит от скорости сгорания топлива. Крутящий момент – результат от действия силы на рычаг. Эта сила в физике считается в ньютонах. Длина плеча коленвала считается в метрах. Поэтому обозначение крутящего момента – ньютон-метр.

Технически, крутящий момент – это усилие, которое должно осуществляться двигателем для разгона и движения машины. При этом сила, оказывающая действие на поршень, пропорциональна объему двигателя.

Формула расчета крутящего момента

Показатель КМ рассчитывается так: мощность (в л. с.) равно крутящий момент (в Нм) умножить на обороты в минуту и разделить на 5,252. При меньших чем 5,252 значениях крутящий момент будет выше мощности, при больших – ниже.

В пересчете на принятую в России систему (кгм – килограмм на метр) – 1кг = 10Н, 1 см = 0,01м. Таким образом 1 кг х см = 0,1 Н х м. Посчитать вращательный момент в разных системах измерений ньютоны/килограммы и т.д. поможет конвертер – в практически неизменном виде он доступен на множестве сайтов, с его помощью можно определять данные по практически любому мотору.

График:

На графике изображена зависимость крутящего момента двигателя от его оборотов

От чего зависит крутящий момент

На КМ будут влиять:

• Объем двигателя.
• Давление в цилиндрах.
• Площадь поршней.
• Радиус кривошипа коленвала.

Основная механика образования КМ заключается в том, что чем больше двигатель по объему, тем сильней он будет нагружать поршень. То есть – будет выше значение КМ. Аналогична взаимосвязь с радиусом кривошипа коленвала, но это вторично: в современных двигателях этот радиус сильно изменить нельзя.

Давление в камере сгорания – не менее важный фактор. От него напрямую зависит сила, давящая на поршень.

Для снижения потерь крутящего момента при тряске машины во время резкого газа можно использовать компенсатор. Это специальный (собранный вручную) демпфер, компенсация которого позволит сохранить вращающий момент и повысить срок эксплуатации деталей.

На что влияет крутящий момент

Главная цель КМ – набор мощности. Часто мощные моторы обладают низким показателем КМ, поэтому не способны разогнать машину достаточно быстро. Особенно это касается бензиновых двигателей.

ВАЖНО! При выборе авто стоит рассчитать оптимальное соотношение вращательного момента с количеством оборотов, на которых чаще всего мотор будет работать. Если держать вращательный момент на соответствующем уровне, это позволит оптимально реализовать потенциал двигателя.

Высокий КМ также может влиять на управляемость машины, поэтому при резком увеличении скорости не лишним будет использование системы TSC. Она позволяет точнее направлять авто при резком разгоне.

Широко распространенный 8-клапанный двигатель ВАЗ выдает вращательный момент 120 (при 2500-2700 оборотах). Ручная коробка или АКПП стоит на машине – не принципиально. При использовании КПП немаловажен опыт водителя, на автоматической коробке плавный старт обеспечивает преобразователь.

Как увеличить крутящий момент

Увеличение рабочего объема. Чтобы повышать КМ используются разные методы: замена установленного коленвала на вал с увеличенным эксцентриситетом (редко встречающаяся запчасть, которую трудно находить) или расточка цилиндров под больший диаметр поршней. Оба способа имеют свои плюсы и минусы. Первый требует много времени на подбор деталей и снижает долговечность двигателя. Второй, увеличение диаметра цилиндров с помощью расточки, более популярен. Это может сделать практически любой автосервис. Там же можно настроить карбюратор для повышения КМ.

Изменение величины наддува. Турбированные двигатели позволяют достичь более высокого показателя КМ благодаря особенностям конструкции – возможности отключить ограничения в блоке управления компрессором, который отвечает за наддув. Манипуляции с блоком позволят повысить объем давления выше максимума, указанного производителем при сборке автомобиля. Способ можно назвать опасным, поскольку у каждого двигателя есть лимитированный запас нагрузок. Кроме того, часто требуются дополнительные усовершенствования: увеличение камеры сгорания, приведение охлаждения в соответствие повышенной мощности. Иногда требуется отрегулировать впускной клапан, иногда – сменить распредвал. Может потребоваться замена чугунного коленвала на стальной, замена поршней.

Изменение газодинамики. Редко используемый вариант, поскольку двигатель – сложная конструкция, созданием которого занимаются профессионалы. Теоретически можно придумать, как убрать ограничения, заложенные конструкторами для увеличения срока эксплуатации двигателя и его деталей. Но на практике, если убрать ограничитель, результат не гарантирован, поскольку поменяются все характеристики: например, динамика вырастет, но шина не будет цепляться за дорогу. Чтобы усовершенствовать двигатель такие образом надо быть не просто автомобильным конструктором, но и математиком, физиком и т.д.

ВАЖНО! Простой способ повысить КМ – использовать масляный фильтр. Он снизит засорение двигателя и продлит срок эксплуатации всех деталей.

Определение крутящего момента на валу

Для измерения крутящего момента на валу автомобильного двигателя применяется множество методик. Это может быть показатель подачи топлива, температуры выхлопных газов и т.д. Такие методы не гарантируют высокой точности.

Распространенный метод повышенной точности – применение тензометрического моста. На вал крепятся тензометры, электрически соединенные по мостовой схеме. Сигнал передается на считывающее устройство.

Измеритель крутящего момента

Главная сложность в измерителе крутящего момента, использующего тензометры, является точность передачи данных. Применявшиеся ранее контактные, индукционные и светотехнические устройства не гарантировали необходимой эффективности. Сейчас данные передаются по цифровым радиоканалам. Измеритель представляет собой компактный радиопередатчик, который крепится на вал и передает данные на приемник.

Сейчас такие устройства доступны по стоимости и просты в эксплуатации. Применяются в основном в СТО.

Датчик крутящего момента

Аналогичные устройства, измеряющие КМ, в автомобиле могут быть установлены не только на коленвал, но и на рулевое колесо. Он ставится на модели машин с электроусилителем руля и позволяет отслеживать работу системы управление автомобилей. При выходе датчика из строя, усилитель, как правило, отключается.

Максимальный крутящий момент

Максимальным называется крутящий момент, представляющий пик, после которого момент не растет, несмотря на количество оборотов. На малых оборотах в цилиндре скапливается большой объем остаточных газов, в результате чего показатель КМ значительно ниже пикового. На средних оборотах в цилиндры поступает больше воздуха, процент газов снижается, крутящий момент продолжает расти.

При высоких оборотах растут потери эффективности: от трения поршней, инерционных потерь в ГРМ, разогрева масла и т.д. будет зависеть работа мотора. Поэтому рост качества работы двигателя прекращается или само качество начинает снижаться. Максимальный крутящий момент достигнут и начинает снижаться.

В электродвигателях максимальный вращательный момент называется «критический».

Таблица марок автомобилей с указанием крутящего момента:

Модели автомобиля ВАЗ	Крутящий момент (Нм, разные марки двигателей)
2107	93 – 176
2108	79-186
2109	78-118
2110	104-196
2112	104-162
2114	115-145
2121 (Нива)	116-129
2115	103-132
2106	92-116
2101	85-92
2105	85-186
Двигатели ЗМЗ
406	181,5-230
409	230
Других популярные в России марки автомобилей
Ауди А6	500-750
БМВ 5	290-760
Бугатти Вейрон	1250-1500
Дэу Нексия	123-150
Киа Рио	132-151
Лада Калина	127-148
Мазда 6	165-420
Мицубиси Лансер	143-343
УАЗ Патриот	217-235
Рено Логан	112-152
Рено Дастер	156-240
Тойота Королла	128-173
Хендай Акцент	106-235
Хендай Солярис	132-151
Шевроле Каптив	220-400
Шевроле Круз	118-200

Какому двигателю отдать предпочтение

Сегодня множество моделей производители оснащают разными типами моторов: бензиновым или дизельным.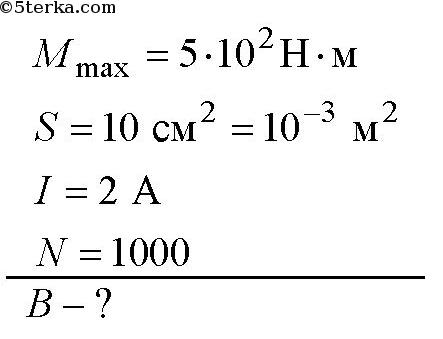 Эти модели идентичны только по цене и другим характеристикам.

Из-за разных типов мотора одна и та же модель может отличаться по показателям мощности мотора и крутящему моменту, при этом разница может быть значительной.

Бензиновый двигатель

Бензиновый двигатель формирует воздушно-топливную смесь, заполняющую цилиндр. Температура внутри него поднимается до примерно 500 градусов. У таких моторов номинальный коэффициент сжатия составляет порядка 9-10, реже 11 единиц. Поэтому, когда происходит впрыск необходимо использование свечей зажигания.

Дизельный двигатель

В цилиндрах работающего на дизеле движка коэффициент сжатия смеси может достигать показателя в 25 единиц, температура – 900 градусов. Поэтому смесь зажигается без использования свечи.

Электродвигатель

Чтобы ответить на вопрос – дизельный, бензиновый или электродвигатель лучше, надо сначала исключить третий вариант, поскольку электродвигатели пока не так распространены, как первые два типа.

ВАЖНО! Что касается выбора между бензиновым и дизельным двигателями, они в первую очередь отличаются мощностью и крутящим моментом. На практике это означает, что при одинаковом объеме двигателя дизельный быстрее разгоняется, а бензиновый позволяет давать более высокую скорость.

Улучшение разгона авто за счет изменения момента вращения

Чем выше показатель крутящего момента – тем быстрее двигатель набирает мощность. Таким образом, вырастет скорость движения. На практике это означает, что, например, во время разгона крутящий момент позволит быстрее обогнать едущий впереди автомобиль.

Чтобы улучшить разгон автомобиля за счет изменения момента вращения, достаточно повысить показатели последнего. Как это сделать – описано выше.

Зависимость мощности от крутящего момента

Крутящий момент, как говорилось выше, это показатель того, с какой скоростью двигатель может набирать обороты. По сути, мощность мотора – прямая производная от КМ на коленвале. Чем больше оборотов – тем выше показатель мощности.

Зависимость мощности от вращательного момента выражается формулой: Р = М*n (Р – мощность, М – крутящий момент, n – количество оборотов коленвала/мин).

Состояние максимального крутящего момента асинхронного двигателя и выражение

В этой статье мы обсудим условия, при которых асинхронный двигатель развивает максимальный крутящий момент. Крутящий момент асинхронного двигателя зависит от тока ротора, коэффициента мощности ротора и потока статора на полюс. Кроме того, ток ротора зависит от скольжения, сопротивления ротора и реактивного сопротивления ротора. Таким образом, можно сказать, что крутящий момент асинхронного двигателя зависит от следующего.

• Поток статора/полюс
• Сопротивление ротора
• Реактивное сопротивление ротора
• Скольжение

Сопротивление ротора, скольжение и реактивное сопротивление ротора вызывают изменение коэффициента мощности асинхронного двигателя. Таким образом, говоря простыми словами, крутящий момент асинхронного двигателя зависит от потока статора, тока ротора и коэффициента мощности ротора.

Крутящий момент асинхронного двигателя

Почему асинхронный двигатель…

Включите JavaScript

Почему асинхронный двигатель имеет низкий коэффициент мощности при холостом ходе

Рабочий момент асинхронного двигателя можно выразить с помощью математической формулы.

Из приведенного выше математического выражения рабочего момента асинхронного двигателя можно сделать следующие выводы.

• При скольжении(s) = 0, Torque(T) = 0
• При нормальной скорости скольжение мало, поэтому sX ₂ пренебрежимо мало по сравнению с R2. Следовательно, крутящий момент прямо пропорционален скольжению.

• Когда скольжение превышает скольжение при полной нагрузке, крутящий момент увеличивается и становится максимальным в определенной точке Максимальный крутящий момент в асинхронном двигателе называется момент отрыва или разрыва. Его значение обычно в два раза превышает значение полной нагрузки, когда двигатель работает при номинальном напряжении и частоте. При более высоком значении скольжения Член 𝑠2𝑋22 быстро увеличивается с более высоким значением скольжения, и этот член становится значимым в уравнении крутящего момента. По сравнению с этим термином 𝑅 ₂ ² очень мал и им можно пренебречь. Таким образом, крутящий момент в этом состоянии обратно пропорционален скольжению.

Вышеупомянутые пункты также можно понять по характеристикам проскальзывания крутящего момента асинхронного двигателя.

• В начале скольжение равно 1 и T=0
• До момента подтягивания момент пропорционален скольжению.
• После точки тягового момента момент обратно пропорционален скольжению.

Условия максимального крутящего момента асинхронного двигателя:

Уравнение крутящего момента асинхронного двигателя:

Уравнение (1) можно записать как;

Знаменатель уравнения (2) может быть записан в квадратной форме,

Мы знаем,

Применение вышеуказанного свойства в уравнении (3). мы получаем;

Развиваемый крутящий момент будет максимальным, если значение правой части уравнения (4) максимально. Это условие возможно, если значение показанного ниже знаменателя равно нулю.

Следовательно, развиваемый крутящий момент асинхронного двигателя максимален, если сопротивление ротора на фазу равно реактивному сопротивлению ротора на фазу в рабочем состоянии.

Альтернативный метод получения условия для максимального рабочего момента асинхронного двигателя

Выражение для крутящего момента асинхронного двигателя в рабочем состоянии имеет вид переменная. Скольжение изменяется при изменении нагрузки на двигатель. Следовательно, скольжение является решающим фактором крутящего момента, создаваемого двигателем. Таким образом, крутящий момент асинхронного двигателя зависит от скольжения. Крутящий момент, создаваемый асинхронным двигателем, максимален, если дифференциация крутящего момента по отношению к скольжению равна нулю.

Подставив значение «T» в приведенное выше уравнение,

Следовательно,

Скольжение, при котором крутящий момент максимален, обозначается как с _м .

Максимальное скольжение представляет собой отношение времени простоя к значениям сопротивления и реактивного сопротивления ротора, когда двигатель создает максимальный крутящий момент.

Выражение для максимального крутящего момента

Максимальный крутящий момент асинхронного двигателя можно получить, подставив максимальное значение скольжения (s _m  = R ₂ /X ₂  ) в уравнении крутящего момента.

Уравнение крутящего момента:

Подставив R ₂  = sX ₂  в приведенное выше уравнение крутящего момента,

Из приведенного выше уравнения видно, что максимальный крутящий момент не зависит от сопротивления ротора.

Скорость двигателя;

Приведенное ниже уравнение показывает скорость вращения ротора при максимальном крутящем моменте.

Заключение о максимальном крутящем моменте асинхронного двигателя

Из вышеизложенного можно сделать следующие выводы.

• Максимальный крутящий момент не зависит от сопротивления цепи ротора.
• Реактивное сопротивление цепи ротора при остановке играет жизненно важную роль в обеспечении максимального крутящего момента. Максимальный крутящий момент, создаваемый двигателем, обратно пропорционален реактивному сопротивлению покоя ротора. Следовательно, индуктивность ротора должна быть как можно меньше.
• Максимальный крутящий момент прямо пропорционален квадрату ЭДС неподвижного ротора (E2).
• Вводя сопротивление в цепь ротора и изменяя сопротивление, можно получить максимальный крутящий момент при любом желаемом скольжении или скорости.

Для развития максимального крутящего момента при запуске асинхронного двигателя сопротивление ротора должно быть высоким и должно быть равно реактивному сопротивлению ротора (X2). Когда двигатель начинает ускоряться, значение сопротивления должно быть уменьшено, чтобы получить крутящий момент в рабочих условиях.

Решенная проблема

Сопротивление и реактивное сопротивление ротора асинхронного двигателя 440 В, 6 полюсов, 3 фазы, 50 Гц, соединенного звездой, составляют 0,02 и 0,15 Ом соответственно. Рассчитайте следующие.

(1) Пусковой момент
(2) проскальзывание, при котором возникает максимальный крутящий момент
(3) скорость, при которой возникает максимальный крутящий момент
(4) максимальный крутящий момент
(5) крутящий момент при полной нагрузке, если проскальзывание при полной нагрузке составляет 4 % . Примите отношение числа оборотов статора к числу оборотов ротора, равное 4.

Данные:
P = 6
Н _с = 120f/P
Н _с = 120 X 50/6
Н _{с = 1} об/мин.
N= 16,66 об/с
R ₂ = 0,02 Ом
X ₂ = 0,15 Ом

Напряжение сети = 440 В, двигатель соединен звездой, следовательно, фазное напряжение равно;

= 440/√3 = 254 В

Коэффициент трансформации (K) = обороты ротора / обороты статора
K = 1/4 = 0,25

Кроме того,

Коэффициент трансформации = напряжение ротора/напряжение статора 2 /E ₁
E ₂ = 0,25 X 254
E ₂ = 63,5 В

(1) При пуске проскальзывание двигателя равно единице.

Следовательно, пусковой момент асинхронного двигателя равен;

(2) скольжение при максимальном крутящем моменте

(3) Скорость, при которой возникает максимальный крутящий момент

(4) Максимальный крутящий момент

(5) Момент при полной нагрузке, если проскальзывание при полной нагрузке составляет 4 %.

s= 0,04

Читать дальше

Похожие сообщения:

Пожалуйста, следите за нами и лайкайте нас:

Условия максимального крутящего момента в трехфазном асинхронном двигателе

какой двигатель работает. Напряжение питания двигателя обычно номинальное и постоянное, и существует фиксированное соотношение между E ₁  и E ₂ . ence E ₂  также является константой. Точно так же R ₂ , X ₂ и n _s являются константами для асинхронного двигателя.

Следовательно, при поиске условия максимального крутящего момента помните, что единственным параметром, который управляет крутящим моментом, является скольжение s.

Математически для максимального крутящего момента мы можем написать,

dT/ds = 0
, где        T = (k s E ₂ ²  R ₂ )/(R

2 0044 2  +(s X ₂ ) ² )

При выполнении дифференциала помните, что E ₂ , R ₂ , X ₂  и k являются константами. Единственная переменная — это скольжение. При изменении нагрузки на двигатель изменяется его скорость и, следовательно, изменяется скольжение. Это скольжение определяет создаваемый крутящий момент в соответствии с нагрузкой.

T = (k s E ₂ ²  R ₂ )/(R ₂ ²  + s ²  2 9004 2

2 0045 )            …….Writing (s X ₂ ) ²   = s ²  X ₂ ²

В качестве обоих

для у/в.

^. . K S E ₂ ² R ₂ (2S x ₂ ² ) — (R ₂ ² + S ² X ₂ ^{4+ S 2 X ₂ 444444444444 2 2 2 X _{2 + S 2 X 2 0045 )(k E 2 2  R 2 ) = 0
. . .               2 s 2  k X 2 2  E 2 2  R 2  – R 2 2  k E 2 2  R 2  – k  s 2 X}}

2 ² E ₂ ² R ₂ = 0
. ^. .               k s ²   X ₂ ² E ₂ ² R ₂ — R ₂ ² K X ₂ ² R ₂ = 0
. ^. . S ² x ₂ ² — R ₂ ² = 0 Взятие K E ₂ ² R ₂ Common.
. ^. .               s ²   = R ₂ ² /X ₂ ²
. ^. .               s = R ₂ /X ₂                  Пренебрегая отрицательным скольжением

Это скольжение, при котором крутящий момент максимален, обозначается как s _m .

.

. .                с _м = R ₂ /X ₂

Это отношение останова к значениям сопротивления и реактивного сопротивления ротора, когда крутящий момент, создаваемый асинхронным двигателем, максимален.

1.1 Величина максимального крутящего момента

Это можно получить, подставив s _m  = R ₂ /X ₂    в уравнение крутящего момента. Обозначается Т _м .

T _M = (K S _M E ₂ ² R ₂ )/(R ₂ ² +(S _M x ₂ ) ^{44444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444445)} +(S _M x _{2 ) +) .}

Из выражения T _m можно заметить, что

1. Обратно пропорционально реактивному сопротивлению ротора.
2. Она прямо пропорциональна квадрату ЭДС, индуцируемой ротором.

в состоянии покоя.
3. Самое интересное наблюдение заключается в том, что максимальный крутящий момент не зависит от сопротивления ротора R ₂ .

Но скольжение, при котором оно происходит, т.е. скорость, при которой оно происходит, зависит от значения сопротивления ротора R ₂ .

Пример 1  : Асинхронный двигатель 400 В, 4 полюса, 3 фазы, 50 Гц, соединенный звездой, имеет сопротивление ротора и реактивное сопротивление на фазу, равные 0,01 Ом и 0,1 Ом соответственно. Определите i) пусковой момент ii) проскальзывание, при котором возникает максимальный крутящий момент iii) скорость, при которой возникает максимальный крутящий момент iv) максимальный крутящий момент v) крутящий момент при полной нагрузке, если проскальзывание при полной нагрузке составляет 4 %. Предположим, что отношение числа оборотов статора к оборотам ротора равно 4,9.0003

Решение . = напряжение линии статора = 400 В
E _{1 фаза} = E _{1 фаза} /√3 = 400/√3 = 230,94 В                Обороты статора = 1/4
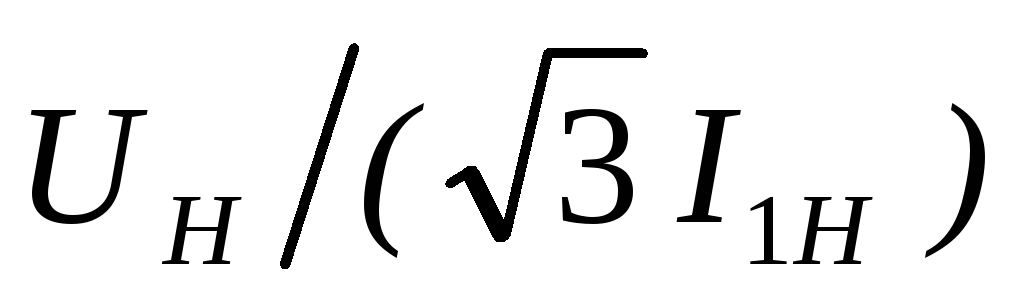. ^. .                       E ₂ = (1/4) x E _{1 фаза} = 230,94/4 = 57,735 В
N _с = 120f/P = 120×50 / 4 = 1500 об/мин.
i) В начале          s =1
. ^. . T _ST = (K E ₂ ² R ₂ )/(R ₂ ² +(x ₂ ) ² ), где K = 3/(2 Z ) ² ), где K = 3/(2 Z _{) s} )
n _s  = N _s /60 = 1500/60 = 25 об/с.
. ^. .                      k = 3/(2π x 25) = 0,01909
. ^. . T _ST = (0,01909 x 57,735

2 x 0,01)/(0,01 ² + 0,1 ² ) = 63,031 N-M

II), на котором максимум Courte Cource occours,
S _{= M 2}

II), на котором максимальное круглое составляет,
S _{= M . 2 /X 2  = 0,01/0,1 = 0,1
%s м = 0,1 x 100 = 10%}

iii) Скорость, при которой возникает максимальный крутящий момент, соответствует скорости,
N = N _с (1 – с _м ) = 1500 (1 – 0,1) = 1350 об/мин.