Кинематическое исследование планетарного редуктора — решение курсовых по ТММ. Публикации.
|
Помогу по ТММ . Если нужна помошь по дифференциальных механизмам и планетарным ступеням — пиши мне вк. Примеры моих работ: Билет1 Билет2 РГР1 РГР2 РГР3 В состав планетарного редуктора, как правило, входят солнечные колеса – колеса у которых оси неподвижные и планетарная ступень, включающая в себя сателлит – колесо с подвижной осью вращения. Кинематическое исследование планетарного редуктора в ТММ сводиться к определению нужного передаточного отношения, частоты вращения выходного вала. В ТММ есть два способа – графический и аналитический. Далее рассмотрим каждый из них по отдельности.
R=mz/2 , где R – радиус колеса, m – модуль колес, z – число зубьев колеса. Для некоторых колёс число зубьев может быть не задано – их определяем из условия соосности. После построения картины линейных скоростей переходим к построению картины угловых скоростей: для этого линии, соответствующие скоростям точек того или иного звена, переносим параллельно самой себе (с помощью рейсшины) в полюс картины угловых ускорений (положение которого выбрали произвольно). Искомое передаточное отношение планетарного редуктора находиться как отношение соответствующих отрезков на картине угловых скоростей. Аналитический метод кинематического исследования планетарного редуктора: Аналитический метод в ТММ существенно отличается от графического: Вычисляются отдельно передаточные отношения дополнительной и дифференциальной частей редуктора. Передаточное отношение дополнительной части находиться как произведение передаточных отношений входящих в нее ступеней (причем передаточное отношение передачи внешнего зацепления отрицательно, внутреннего – положительна).Для дифференциальной части редуктора составляется формула Виллиса (останавливается водило). Далее составляются уравнения связи. Решая совместно эти уравнения находят передаточное отношение планетарного редуктора, и другие искомые величины. |
Планетарные редукторы — принцип работы, механизм действия, преимущества и недостатки
Планетарная передача — это механическая передача на основе вращательного движения, способная в пределах одной оси изменять, складывать и раскладывать угловые скорости и крутящий момент.
Планетарные передачи имеют небольшие размеры, обеспечивают большое передаточное отношение и крутящий момент, превосходя по характеристикам зубчатые передачи с фиксированной осью.Простой планетарный редуктор изображен со стороны подачи момента. Двойные роликовые подшипники на выходе позволяют изолировать прямозубые шестерни от воздействия внешних поперечных нагрузок.
Основой планетарной передачи является водило.
Планетарная передача имеет соосные валы и корпус цилиндрической формы, являясь компактной альтернативой стандартным редукторам на основе колеса и шестерни. Планетарная передача используется во многих устройствах — от электрических шуруповертов до силовых приводов бульдозеров, то есть в оборудовании, к которому предъявляются повышенные требования по компактности и легкости при обеспечении больших передаточных отношений и крутящего момента. Разберемся в принципах работы планетарной передачи. Рассмотрев конструкцию и механику планетарных редукторов, можно выявить несколько не очевидных на первый взгляд факторов.
Конфигурация
Типичная планетарная передача включает в себя три группы зубчатых колес с различными степенями свободы. Планетарные шестерни (сателлиты) вращаются вокруг осей, которые, в свою очередь, вращаются вокруг солнечной шестерни, имеющей фиксированную ось вращения. Большое центральное зубчатое колесо с внутренними зубьями (эпицикл) имеет фиксированное положение и входит в зацепление с сателлитами.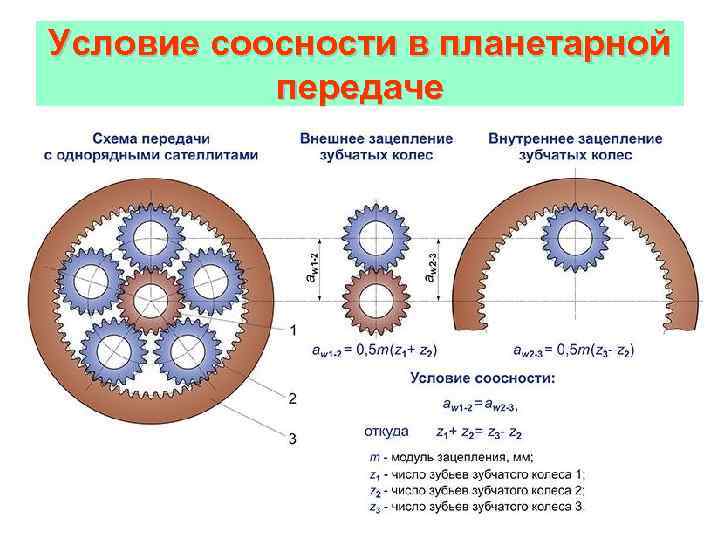
Концентричность сателлитов относительно солнечного колеса и эпицикла позволяет передавать крутящий момент по прямой линии. Многие силовые передачи «удобно» выровнены по прямой линии, а отсутствие смещенных валов не только экономит пространство, но и избавляет от необходимости перенаправления мощности или изменения расположения других элементов.
В простой планетарной передаче входная мощность проворачивает солнечное колесо с частотой вращения. Сателлиты, расположенные вокруг центральной оси вращения, входят в зацепление и с солнечным колесом, и с эпициклом, поэтому они вращаются по орбите. Все сателлиты монтируются на одном вращающемся звене, называемом водилом. При этом водило вращается с низкой частотой и высоким крутящим моментом.
Однако, использование фиксированного элемента не обязательно. В дифференциальных передачах все элементы вращаются. Подобные планетарные передачи позволяют реализовать механизм с одним выходом и двумя источниками крутящего момента, либо систему с одним источником момента и двумя выходами.
Например, в автомобилях используется приводной дифференциал, который представляет собой коническую планетарную передачу — используются две выходные оси для передачи крутящего момента на колеса автомобиля, которые вращаются независимо с учетом угла расположения колес. Механизмы с коническими планетарными передачами работают по принципу, аналогичному механизмам с параллельными валами.
Даже простая планетарная передача имеет два входа; фиксированный эпицикл имеет постоянную нулевую угловую скорость.
Конструкторы имеют возможность использовать более сложные планетарные механизмы. Сложные планетарные передачи включают в себя минимум два сателлита, установленных в линию на одном валу и вращающиеся вокруг своей оси и по орбите с одинаковой скоростью, но входящими в зацепление с разными шестернями. Такие сателлиты могут иметь различное число зубьев, как и шестерни, с которыми они входят в зацепление. Подобные реализации обеспечивают дополнительные возможности с точки зрения механики узлов и позволяют значительно увеличить передаточное отношение каждой ступени.
Увеличение степени редуцирования
2. Планетарная передача (приводное солнечное колесо)
Сателлиты имеют небольшой размер и большое количество зубьев, поэтому выходной вал может сделать один оборот за определенное количество оборотов приводного вала. Для реализации сравнимого передаточного отношения с использованием обычной передачи необходимо использовать колесо большого размера, которое будет входить в зацепление с маленькой шестерней.
Простая планетарная передача, как правило, имеет передаточное число до 10:1. Сложные планетарные механизмы, имеющие гораздо более замысловатые конструкции, могут обеспечивать значительно большую степень редуцирования.
Другим вариантом является встраивание обычной зубчатой передачи в планетарную. Например, входной вал с высокой частотой вращения может соединяться со стандартной передачей с фиксированными осями вращения, после чего крутящий момент передается на планетарную передачу. Такая конфигурация называется гибридной и является упрощенной альтернативой установке дополнительных планетарных ступеней, либо применяется в случаях, когда частота вращения входного вала оказывается слишком высокой для планетарной передачи. Кроме того, такое использование обычной передачи требует смещения оси вращения. Для получения необходимого угла на входе планетарной передачи иногда используются конические или гипоидные передачи.
Передача крутящего момента
3. Передача с фиксированными осями (с приводной шестерней)
Поскольку сателлиты планетарной передачи входят в зацепление с солнечным колесом и эпициклом в нескольких местах, для перемещения нагрузки задействуется большее число зубьев по сравнению с обычными передачами. Благодаря этому планетарная передача состоит из зубчатых колес меньших размеров (но включает большее их количество). Аналогично, радиальные плечи водила передают значительный момент на выходной вал — это другое преимущество концентрической компоновки механизма.
Менее очевидным, но более значительным является тот факт, что благодаря нескольким равномерно расположенным сателлитам (типовая реализация) подшипники выходного и входного валов испытывают меньшие радиальные нагрузки, появляющиеся в результате действия радиальных и тангенциальных ответных сил, поскольку эти силы отсутствуют.
Кроме того, поскольку на подшипники не действуют подобные силы, существует меньшая вероятность повреждения корпуса.
С увеличением числа сателлитов улучшаются нагрузочные характеристики и жесткость на скручивание; чем более рассеянной является нагрузка, тем меньше изнашиваются и повреждаются зубья шестерен. Обычно в планетарных передачах используются три сателлита, зачастую — большее количество, а иногда и меньшее. При этом повторимся, что, как правило, сателлиты равномерно расположены вокруг солнечного колеса.
Для восприятия нагрузок, превышающих возможности прямозубых передач, могут использоваться косозубые передачи сравнимого размера и характеристик, поскольку зубья их шестерен расположены под углом, что обеспечивает вхождение в зацепление большего количества зубьев одновременно. Однако косозубые планетарные передачи подвержены радиальным нагрузкам, которые не нивелируется сателлитами, поэтому подшипники должны быть рассчитаны с учетом этих дополнительных нагрузок.
Износ
Говоря о сроке службы, следует отметить, что планетарные передачи прекрасно распределяют нагрузку между основными элементами, о чем свидетельствуют их небольшие размеры. Если используются компоненты одинакового качества, потенциально слабым местом являются подшипники, на которых крепятся сателлиты.
Часто пространство для установки редуктора весьма ограничено, но планетарные передачи имеют компактные размеры и в них используются подшипники малых типоразмеров в сравнении с обычными передачами с большими подшипниками. Также не стоит забывать о том, что сателлиты нивелируют радиальные нагрузки только на центральные валы; фактически, подшипники отдельных сателлитов, приводящих в движение водило, подвержены радиальным нагрузкам.
В этих подшипниках может наблюдаться термическая и циклическая усталость, обусловленная ограниченным распределением нагрузки и высокой частотой вращения. Более того, большие частоты вращения и тяжелые сателлиты становятся причиной возникновения центробежной силы, значительно увеличивающей нагрузку на механизм.
Однако это не означает, что степень надежности подшипников сателлитов не может превышать надежность других элементов. Очевидно, что использование высококачественных прецизионных подшипников при посредственном качестве зубчатых колес не соответствует принципу равномерности качества элементов механизма.
Балансировка сателлитов
Нагрузка на сателлиты в реальных рабочих условиях не является идеально сбалансированной. Один из сателлитов может случайным образом оказаться ближе или дальше от оси солнечного колеса, либо ось водила может иметь небольшое отклонение. При низком качестве изготовления и увеличении числа сателлитов степень разбалансированности увеличивается.
В некоторых случаях дисбаланс не оказывает значительного влияния и является допустимым для нормальной работы механизма. Сателлиты могут притираться и, в результате, более равномерно распределять нагрузку. Однако некоторые конструкции могут быть чувствительны даже к небольшой разбалансировке и требуют применения высокоточных элементов и узлов; точное расположения осей сателлитов вокруг оси солнечного колеса может являться ключевым фактором надежности и работоспособности механизмов.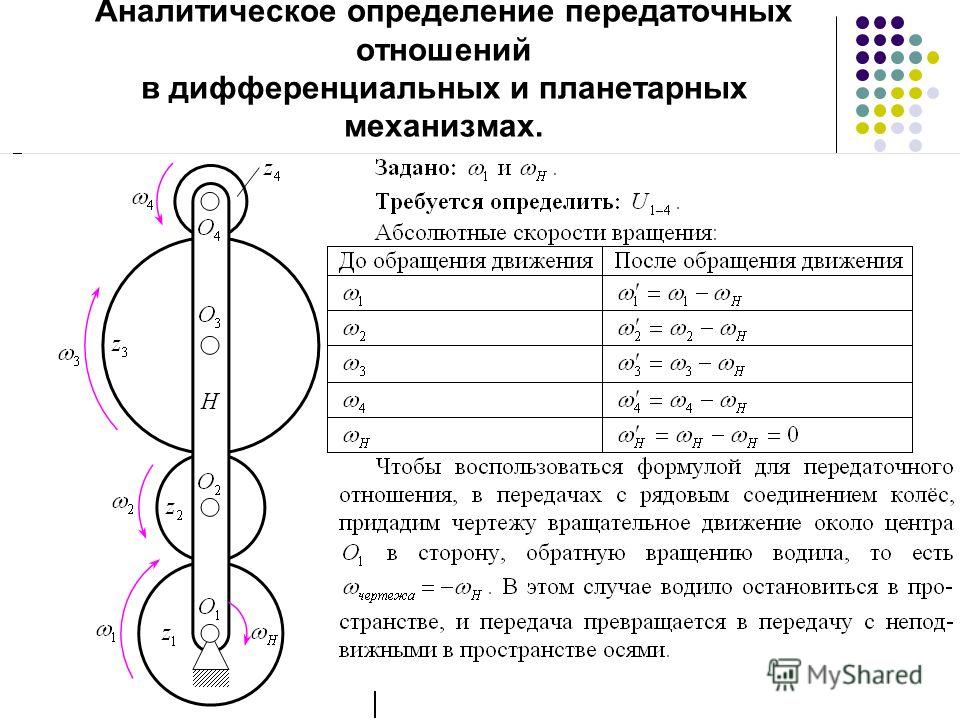
Другими способами балансировки является использование плавающих балансиров или «мягких» вспомогательных элементов, допускающих небольшое радиальное перемещение солнечного колеса или водила. В данном случае элементы могут непрерывно сдвигаться для более равномерного распределения нагрузки. Такая схема является достаточно распространенной, однако жесткая сборка имеет определенные преимущества, поэтому решение не всегда является очевидным.
Шум
4. На рисунке показан пример соосного дифференциала, включающего в себя сложную планетарную передачу со всеми вращающимися компонентами. Составные сателлиты вращаются с одинаковой скоростью, входя в зацепление с двумя различными солнечными колесами. Эти колеса являются косозубыми. В данном случае в качестве водила выступает корпус дифференциала. В конструкции отсутствует эпицикл и два солнечных колеса посажены на два отдельных концентрических вала.
Планетарная передача не является излишне шумной, причем зачастую она работает даже тише, чем обычная зубчатая передача.
Зубчатые колеса меньшего размера являются причиной меньшей окружной скорости на начальной в сравнении с обычными передачами. Однако, большое число зубьев сателлитов, вступающих в зацепление с каждым оборотом вала, генерирует шум, особенно на высоких скоростях. При этом зацепление на круговой орбите еще более усложняет ситуацию. Очевидным решением является использование прямозубых шестерен высокого качества. Однако применение косозубых шестерен с постепенным зацеплением в некоторых случаях может оказаться более предпочтительным решением.
Другим способом снижения шума является проектирование механизма таким образом, чтобы обеспечить смещение фазы выхода из зацепления сателлитов относительно друг друга. Также может помочь демпфирование, предотвращающее появление резонанса.
Нагрев
5. Показанные на рисунке редуктор состоит из трех различных типов передач, включая простую косозубую планетарную передачу для передачи момента под прямым углом. Рассмотрим роль каждого типа передач: обычная косозубая является причиной нарушения соосности валов (нравится вам это или нет), но отлично подходит для восприятия высокой частоты вращения на входе и немного понижает его частоту; коническая передача плавно и эффективно поворачивает угол с дальнейшим снижением частоты вращения; компактная планетарная передача обеспечивает окончательное снижение частоты вращения, обеспечивая высокий крутящий момент.
Планетарная зубчатая передача, работающая на высоких скоростях в непрерывном режиме, генерирует большое количества тепла, которое требует отвода. В обычной зубчатой передаче для работы под нагрузкой зачастую требуется применение больших зубчатых колес с соответствующей площадью поверхности, через которую и отводится тепло. Компактность планетарной передачи ограничивает отвод тепла, что требует дополнительного теплоотвода; для этого может использоваться вентилятор или система циркуляции жидкости через теплообменник. При непрерывной работе механизм имеет меньше возможностей для охлаждения, поэтому при недостаточном теплоотводе в такой планетарной передаче вы будете вынуждены снизить допустимую частоту вращения. Либо, как уже упоминалось выше, перед планетарной передачей можно использовать передачу другого типа для снижения входной частоты вращения, несмотря на то, что это усложняет конструкцию.
Диапазон частоты вращения планетарной передачи в значительной степени зависит от конкретного применения.
Зачастую, размер редуктора сильно влияет на максимально допустимую частоту вращения, поскольку высокая окружная скорость на начальной окружности может привести к повышенному тепловыделению, превышающему охлаждающий эффект большой площади поверхности. Действительно, существуют планетарные передачи, которые работают на частоте в несколько десятков тысяч оборотов в минуту.
DARXTON
Планетарные редукторы — обзор основных критериев проектирования и новые возможности для определения размеров. — ранжирование задач.
| Скачать эту статью в формате .PDF Этот тип файла включает в себя графику и схемы высокого разрешения, если это применимо. |
Например, определенные типы планетарных редукторов:
• Круглосуточная работа семь дней в неделю в течение более 30 000 часов при картонной упаковке.
Редукторы со смазкой на весь срок службы не требуют технического обслуживания, а высокое отношение крутящего момента к размеру обеспечивает компактность и малую площадь основания машины.
• Помогает достичь точности в пределах нескольких десятитысячных дюйма на станках плазменной резки благодаря исключительно малому люфту. Винтовая зубчатая передача обеспечивает быстрое позиционирование и плавное движение, а герметичные редукторы защищают от абразивной пыли, образующейся во время резки.
• Ограничьте шум и вибрацию и соблюдайте строгие требования по люфтам в сканирующих столах для пациентов с сердечно-сосудистыми заболеваниями.
• Оборудование для пищевой промышленности позволяет нарезать мясо, хлеб и замороженные продукты со скоростью до четырех кусочков в секунду. Также доступны тонкие прямоугольные конструкции, которые помещаются в корпус машины и обеспечивают тихую и плавную работу.
Основы планетарной передачи — передаточные числа, углы наклона винтов, осевые нагрузки, выпуклость Планетарный редуктор получает высокоскоростную передачу с низким крутящим моментом, например, от электродвигателя, затем увеличивает крутящий момент и снижает скорость на выходе редуктора соотношение.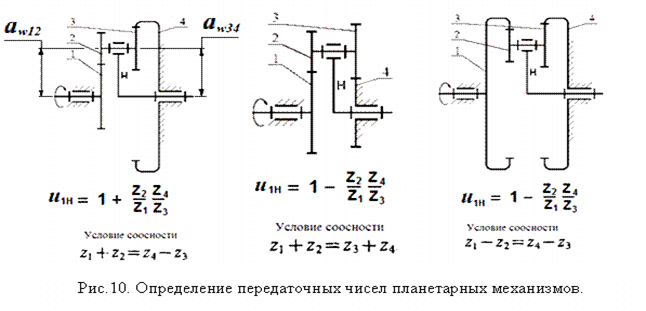
Это позволяет двигателям работать на более высоких и эффективных оборотах в оборудовании, работающем на низких скоростях. Это также снижает инерцию, отражающуюся обратно на двигатель, повышая стабильность. А использование планетарного редуктора часто позволяет машиностроителям уменьшить размер и стоимость оборудования для управления движением.
Планетарные передачи с косозубыми шестернями, а не прямозубыми, имеют большее передаточное отношение. Коэффициент контакта — это количество зубьев в зацеплении в любой момент времени. В то время как типичная прямозубая передача имеет коэффициент контакта 1,5, косозубая передача увеличивает его более чем вдвое до 3,3. Преимущества более высоких коэффициентов контакта:
Редуктор Micron EverTrue предназначен для непрерывной работы. Он может работать без остановок, не превышая 140 ° F, и прослужит более 30 000 часов. • На 30–50 % больше крутящего момента, чем у эквивалентной цилиндрической планетарной передачи.
• Лучшее распределение нагрузки, что увеличивает срок службы.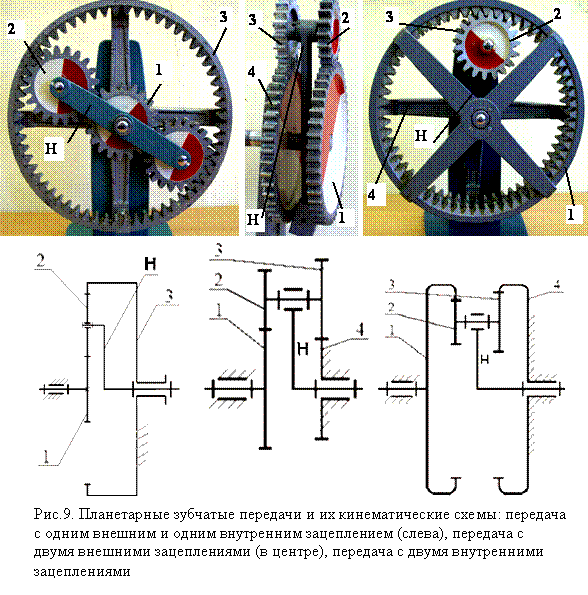
• Более плавная и тихая работа.
• Люфт уменьшен на целых 2 угловых минуты.
Угол наклона зубчатой рейки также оказывает существенное влияние на производительность, поскольку чем больше угол, тем больше зубьев одновременно находится в зацеплении. Таким образом, увеличение угла наклона винтовой линии с типичных 12° до 15° повышает крутящий момент на 17–20%; и на целых 40% по сравнению с прямозубыми цилиндрическими зубчатыми колесами. Шестерни с углом подъема спирали 15° также издают меньше шума.
Зубья косозубых шестерен создают осевые нагрузки на вал двигателя. Подшипники редуктора должны компенсировать эти нагрузки. Цилиндрические редукторы, в которых используются шарикоподшипники с незначительной осевой нагрузкой или вообще без нее, могут привести к преждевременному выходу из строя подшипника двигателя или шестерни. Лучше использовать конические роликоподшипники, например, в редукторах Micron Helical, чтобы полностью компенсировать осевые нагрузки.
Передаточные числа одноступенчатых планетарных редукторов варьируются от 3:1 до 10:1.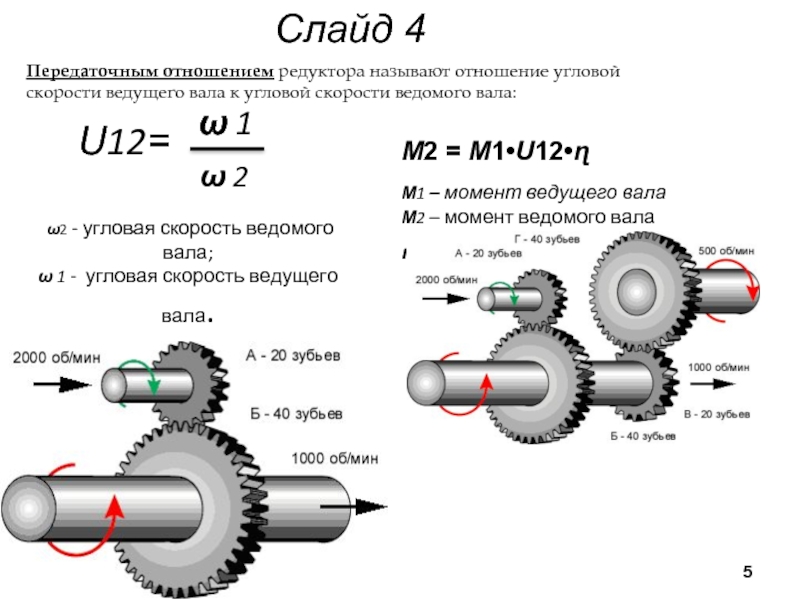
Передаточное отношение не может превышать 10:1, потому что шестерни могут быть сделаны очень маленькими. Передаточное число больше 10:1 возможно при использовании дополнительной планетарной ступени, хотя обычно это увеличивает длину и стоимость. Планетарные конструкции также не могут иметь передаточное число менее 3:1, потому что тогда шестерня и внешнее зубчатое колесо должны быть почти одинакового размера, не оставляя места для планетарных шестерен. Передаточные числа от 4:1 до 8:1 обеспечивают наилучшее сочетание размера шестерни и планетарной передачи, производительности и срока службы.
Выпуклость включает небольшое изменение профиля зуба шестерни для улучшения выравнивания зубчатого зацепления, увеличения допустимого крутящего момента и снижения шума. Это также улучшает распределение нагрузки на боковую поверхность зуба, тем самым сводя к минимуму зоны высокого напряжения, которые могут вызвать питтинг на поверхности.
Планетарные передачи преобразуют высокоскоростные входные сигналы с низким крутящим моментом в низкоскоростные выходные сигналы с высоким крутящим моментом.
Для эффективной работы планетарного редуктора необходим некоторый зазор. Зазор предотвращает чрезмерный нагрев и износ шестерен, а также обеспечивает хорошую смазку. Но небольшой зазор между зубьями шестерни приводит к холостому ходу. Редукторы реального мира также не могут иметь бесконечную жесткость на кручение, поэтому закручивание (изгиб) в редукторе создает дополнительные потери движения.
При выборе редуктора важно знать, как разные производители измеряют люфт. Строгих стандартов, регламентирующих, как измерять люфт, не существует. Это может привести к путанице и заблуждениям. Некоторые производители измеряют и усредняют четыре или более точек на выходном валу, чтобы получить спецификацию люфта. Используя этот метод, устройство с измерениями люфта 4, 6, 10 и 12 угловых минут будет иметь рейтинг 8 угловых минут. Инженеры Thomson считают, что люфт должен основываться на наибольшем измерении на выходном валу, поэтому приведенный выше пример дает оценку 12 угловых минут.
Кроме того, некоторые производители применяют 2 % от номинального крутящего момента для создания рейтинга люфта, в то время как другие применяют меньшее значение.
Последний дает более низкие измерения люфта и не дает истинных оценок люфта в течение всего срока службы продукта.
Люфт со временем будет увеличиваться. Планетарный редуктор может иметь 8 угловых минут люфта из коробки, но, например, 15 угловых минут после шести месяцев использования. Поэтому то, насколько хорошо планетарный редуктор сохраняет точность в течение всего срока службы, является важным фактором для большинства пользователей.
Размер и выбор планетарного редуктора Планетарные редукторы со спиральным венчиком обеспечивают плавное движение с малым люфтом, что позволяет станкам плазменной резки сохранять точность в пределах нескольких десятитысячных дюйма.Правильный выбор редуктора и его точный размер имеют решающее значение для обеспечения длительного и надежного срока службы. В качестве отправной точки конструкторы могут приблизить требуемый размер редуктора из:
T r = T m × r × e
, где T r = крутящий момент приложения, T м = непрерывный крутящий момент, r = передаточное отношение и e = эффективность.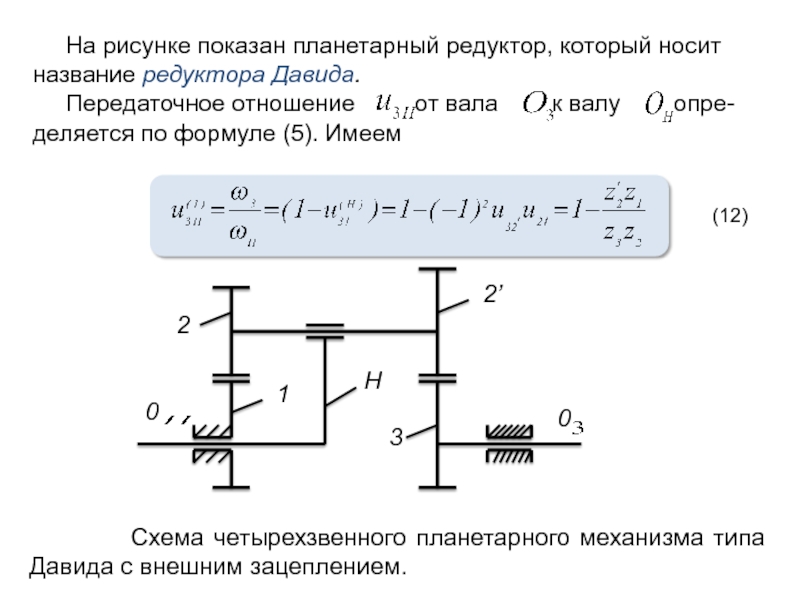
Однако для точного определения размера редуктора инженеры должны учитывать полный профиль движения, включая скорость, крутящий момент, ускорение, замедление и частоту циклов. И они должны применять понижающий коэффициент для условий высокой цикличности. (Типичные значения показаны в таблице.)
Для безостановочных приложений с длительным режимом работы коэффициенты снижения номинальных характеристик не требуются. В этих случаях наиболее распространенной проблемой является перегрев, который разрушает смазку и приводит к выходу из строя шестерни. Высокопроизводительные редукторы, такие как Micron EverTrue, рассчитаны на работу в режиме 24/7, работу при температуре до 140°F и срок службы более 30 000 часов.
Онлайн-инструменты для выбора и определения размеров могут сэкономить время, позволяя инженерам найти и сравнить планетарные редукторы, подходящие для конкретного применения. (Подробнее см. на боковой панели.)
Устранение неисправностей Планетарная передача Некоторые проблемы могут возникнуть в редукторах, которые не подобраны по размеру и не установлены должным образом.
Шум редуктора
Несоответствующая входная скорость, передаточное число редуктора, выходной крутящий момент, радиальные и осевые нагрузки, а также ошибки монтажа могут способствовать возникновению шума редуктора. Но правильный монтаж имеет решающее значение для минимизации шума и максимизации производительности. Многие редукторы необходимо устанавливать на серводвигатель в вертикальном положении. Это позволяет валу двигателя центрировать редуктор. После установки на двигатель редуктор можно использовать в любом положении.
Трение в редукторе
Избыточное количество смазки, компоненты с недопустимыми допусками и плохое качество шестерни или подшипника могут вызвать чрезмерное трение и сопротивление. Ищите производителей редукторов, которые проверяют каждый редуктор на входное сопротивление перед отправкой. Каждый размер и соотношение имеют приемлемый диапазон сопротивления, и пиковые уровни следует измерять в обоих направлениях.
Уплотнение редуктора
Если требуется защита от пыли, грязи и воды, имейте в виду, что сочетание двигателя IP65 и редуктора IP65 не всегда обеспечивает степень защиты IP65.
Посмотрите внимательно, как герметизирован интерфейс между двигателем и редуктором. Наилучшим подходом является использование уплотнительных колец между всеми корпусами для защиты IP65 на всей сборке.
Новый тип планетарного редуктора, Micron AquaTrue, соответствует требованиям IP67 для обработки, упаковки и розлива пищевых продуктов и напитков благодаря круглому корпусу из нержавеющей стали без внешних швов. Такие редукторы могут выдерживать воздействие едких чистящих химикатов и промывки под высоким давлением, что дает инженерам возможность гибкого монтажа без дополнительных затрат и сложности компонентов, таких как кожухи, экраны и механические трансмиссии.
Смазка редуктора
Масло или смазка могут эффективно смазывать планетарные редукторы. Преимущество консистентной смазки состоит в том, что она обеспечивает смазку на весь срок службы редуктора, что устраняет потребность в техническом обслуживании. Смазка позволяет производить монтаж в любом положении и устраняет опасения по поводу утечек.
Масло требует технического обслуживания и повторной смазки, обычно каждые несколько тысяч часов. Утечки всегда являются проблемой при смазке маслом. Ориентация с масляной смазкой обычно ограничена, должна быть указана при заказе и, как правило, не может быть изменена. Распространенным заблуждением является то, что маслонаполненные узлы всегда работают холоднее, чем шестерни с консистентной смазкой. На самом деле, уплотнение, необходимое для маслонаполненного редуктора, часто выделяет больше тепла, чем масло сохраняет.
| Онлайн-выбор и определение размера — попробуйте один вариант Онлайн-инструменты для определения размеров и выбора редуктора упрощают процесс поиска нужного редуктора для применения. Одним из комплексных инструментов для определения размеров является Micron Motioneering. Его режим Sizing and Selection позволяет пользователям вводить параметры приложения, такие как скорость, выходной крутящий момент, радиальные и осевые нагрузки, и инструмент рекомендует редукторы, которые подходят для конкретного применения. На первом экране определения размера и выбора инженеры должны ввести четыре важных элемента информации: 1. Тип или ориентация редуктора (в линию или под прямым углом). Угловые редукторы предлагаются в трех вариантах: стандартный вал, двойной вал и полый вал. 2. Тип приложения. Пользователи выбирают между «Циклической работой» и «Непрерывной работой». Любая работа, выполняемая в одном направлении в течение 4 часов и более без остановки или изменения скорости, считается непрерывной. Все другие приложения, включая машины, которые работают более 4 часов, но меняют направление, считаются циклическими. 3. Требования к люфту делятся на три класса: 4. Соотношение. В этот момент инструмент показывает пользователям доступные коэффициенты для указанных комбинаций. Например, если выбрать линейную ориентацию, соотношения 1:1 и 2:1 будут выделены серым цветом, поскольку они доступны только в прямоугольных версиях. Далее у пользователей есть два способа ввести требования к крутящему моменту и скорости. Первый вариант — ввести их как максимальный крутящий момент и число оборотов в минуту. Можно ввести либо входную, либо выходную скорость вращения, и инструмент рассчитает другую. Для более сложных приложений пользователи могут создать полный профиль движения. Для каждого сегмента профиля движения требуются: скорость в начале и конце сегмента, продолжительность и крутящий момент во время сегмента. После указания этих параметров пользователи могут ввести радиальные или осевые нагрузки, которые могут присутствовать. Выбор опоры двигателя является последним шагом. Крепления доступны от более чем 300 производителей. Пользователи просто выбирают двигатель из раскрывающегося меню, и инструмент генерирует номер детали крепления двигателя. Размеры двигателя также будут отображаться на экране для справки. Если требуемый двигатель отсутствует в списке, инструмент имеет возможность вручную ввести размеры двигателя. Критические размеры, такие как диаметр и длина вала, окружность болта и диаметр направляющей втулки, используются для определения номера комплекта крепления двигателя, необходимого для редуктора. Пользователи могут вводить размеры в английских или метрических единицах. После ввода всех параметров применения инструмент суммирует доступные редукторы, соответствующие критериям применения, отсортированные по цене от самых экономичных до самых дорогих. В нем также указан коэффициент безопасности между требуемым крутящим моментом и номинальным крутящим моментом каждого редуктора. Режим «Выбор редуктора по номеру модели» является опцией, когда требуемый редуктор уже известен. Он позволяет пользователям просматривать цены, спецификации каталогов и сроки выполнения заказов, а также загружать модели САПР. Дизайнеры нажимают на семейство редукторов и выбирают тип продукта, размер рамы, передаточное число и комплект крепления двигателя. Если комплект крепления двигателя неизвестен, пользователи могут ввести размеры, как описано выше. |
Вот посмотрите, как это работает.
После выбора продукта пользователи могут загрузить 2D- или 3D-модель, запросить расценки или сохранить выбор.© Penton Media, Inc., 2012.
Планетарные шестерни – мастер-класс для инженеров-механиков
Я не думаю, что найдется инженер-механик, который не питает слабость к шестерням. Есть что-то во вращающихся кусочках металла (или какого-либо другого материала), сцепленных вместе, завораживающее зрелище, открывающее так много функциональных возможностей. Особенно завораживают планетарные передачи, где шестерни не только вращаются, но и вращаются вокруг центральной оси.
В этой статье мы рассмотрим особенности планетарных передач с прицелом на изучение определенного семейства планетарных передач, иногда называемых «дифференциальными планетарными».
Планетарные передачи
Планетарные передачи обычно состоят из трех частей; Одна солнечная шестерня в центре, внутренняя (кольцевая) шестерня снаружи и некоторое количество планет, которые находятся между ними. Обычно планеты имеют одинаковый размер, находятся на общем расстоянии от центра планетарной передачи и удерживаются водилом планетарной передачи.
В вашей базовой конфигурации зубчатый венец будет иметь количество зубьев, равное числу зубьев солнечной шестерни, плюс две планеты (хотя небольшое изменение может иметь преимущества) просто потому, что линия, проходящая прямо через центр от одной конец зубчатого венца к другому будет охватывать солнечную шестерню в центре и место для планеты на обоих концах. Планеты обычно располагаются через равные промежутки вокруг Солнца.
Для этого общее количество зубьев в зубчатом венце и солнечной шестерне, разделенное на количество сателлитов, должно равняться целому числу. Конечно, планеты должны быть разнесены достаточно далеко друг от друга, чтобы они не мешали.
Эта компоновка дает несколько преимуществ по сравнению с другими возможными компоновками, включая компактность, возможность использования общего центрального вала для солнца, зубчатого венца и водила планетарной передачи, высокую «плотность крутящего момента» из-за того, что нагрузка распределяется между несколькими сателлитами, и тангенциальную силы между шестернями уравновешиваются в центре шестерен из-за равных и противоположных сил, распределенных между зацеплениями между сателлитами и другими шестернями.
Передаточные числа стандартных планетарных редукторов
Солнечная шестерня, зубчатый венец и водило планетарной передачи обычно используются в качестве входных/выходных элементов зубчатой передачи.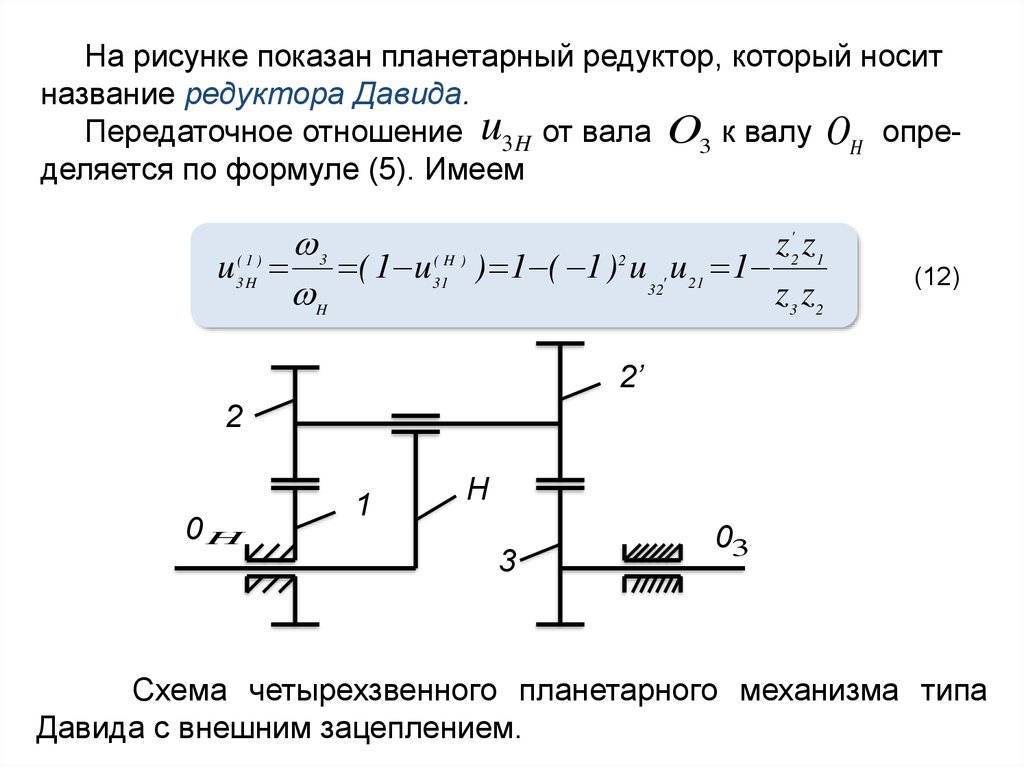
В вашем стандартном планетарном редукторе одна из частей удерживается неподвижно, что упрощает работу и дает вам один вход и один выход. Соотношение для любой пары может быть выработано индивидуально.
Например, если водило удерживается неподвижно, зубчатые колеса по существу образуют стандартную непланетарную зубчатую передачу. Планеты будут вращаться в направлении, противоположном солнцу, с относительной скоростью, обратно пропорциональной отношению диаметров (например, если солнце в два раза больше диаметра планет, солнце будет вращаться со скоростью, вдвое меньшей, чем у планет). Поскольку внешнее зубчатое колесо, находящееся в зацеплении с внутренним, вращается в том же направлении, зубчатый венец будет вращаться в том же направлении, что и сателлиты, и опять-таки со скоростью, обратно пропорциональной отношению диаметров.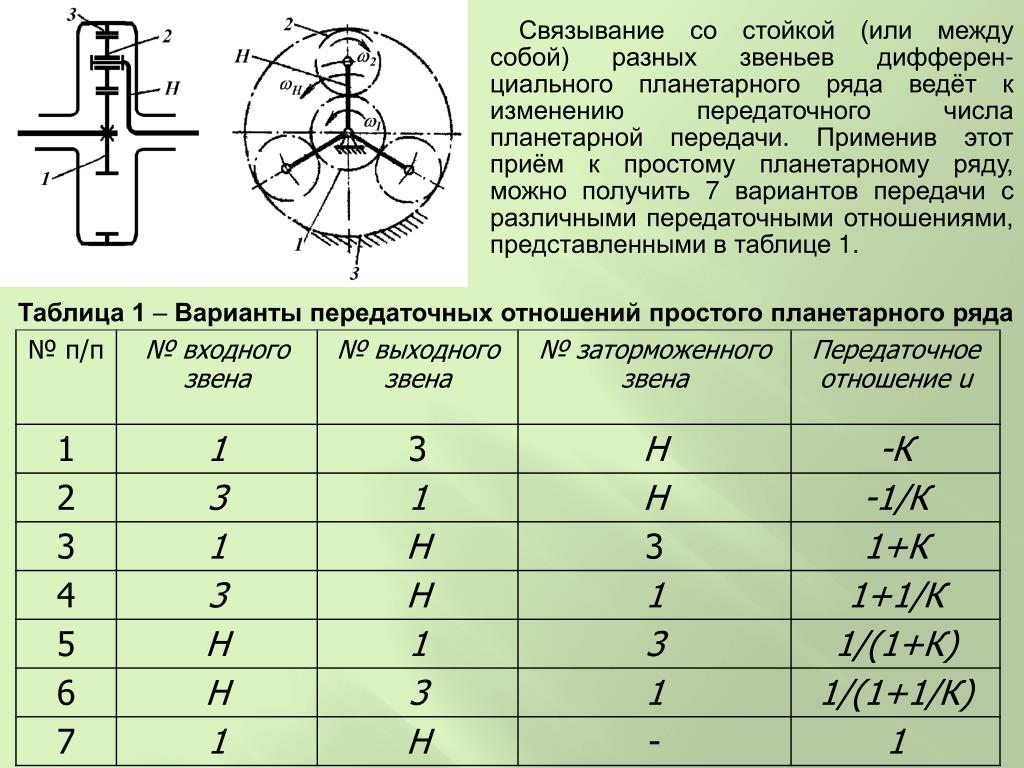
Таким образом, передаточное отношение солнечной шестерни относительно кольца равно -(D солнце /D планета )*(D планета /D кольцо ), или просто -(D солнце /D кольцо ). Это обычно выражается как обратная величина, называемая передаточным отношением, которое в данном случае равно -(D Ring /D Sun ).
Еще один пример; если кольцо удерживается неподвижно, сторона планеты со стороны кольца также не может двигаться, и планета будет катиться по внутренней стороне зубчатого венца. Тангенциальная скорость в зацеплении с солнечной шестерней будет одинакова как для Солнца, так и для планеты, а центр планеты будет двигаться в два раза меньше, находясь на полпути между точкой, движущейся с полной скоростью, и точкой, не движущейся вообще. . Солнце будет вращаться со скоростью вращения относительно скорости в сетке, деленной на диаметр солнца. Носитель будет вращаться со скоростью относительно скорости в
центр планет (половина скорости сетки) разделить на диаметр носителя.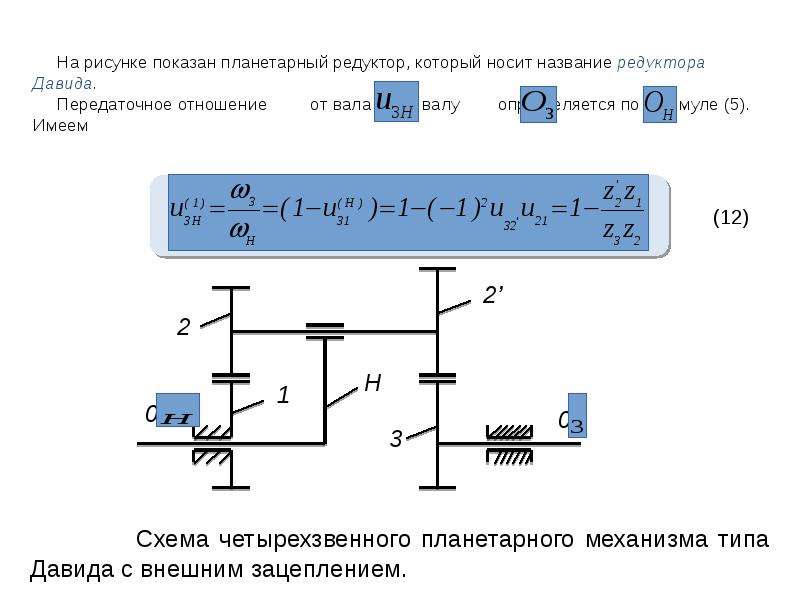
Таким образом, передаточное отношение будет D Carrier /(D Sun /0,5) или просто 2*D Carrier /D Sun .
Метод суперпозиции для определения передаточных чисел
Существует, однако, обобщенный метод для определения передаточного числа любого планетарного ряда без необходимости выяснять, как интерпретировать физическую реальность каждого случая. Это называется «суперпозиция» и работает по принципу: если вы разбиваете движение на разные части, а затем соединяете их вместе, результат будет таким же, как и исходное движение. Это тот же принцип, по которому работает сложение векторов, и не будет преувеличением утверждать, что то, что мы здесь делаем, на самом деле является сложением векторов, если вы приступите к делу.
В этом случае мы разобьем движение планетарного набора на две части. Первый — если заморозить вращение всех шестерен относительно друг друга и вращать водило планетарной передачи. Поскольку все шестерни заблокированы, все будет вращаться со скоростью носителя.
Второе движение — заблокировать водило и повернуть шестерни. Как отмечалось выше, это формирует более типичный набор шестерен, и передаточные числа могут быть получены в зависимости от различных диаметров шестерен. Поскольку мы комбинируем движения а) ничего, кроме держателя картриджа, и б) всего, кроме держателя картриджа, мы охватываем все движения, происходящие в системе.
Информация собрана в таблицу, в которой указано значение скорости для каждой части, а передаточное отношение при использовании какой-либо части в качестве входной, а любой другой части в качестве выходной может быть получено путем деления скорости на входе на скорость выход.
Например, если мы обозначим вращение носителя как «x», а вращение солнца как «y», для вашего базового устройства система выдаст следующую таблицу:
Давайте сравним два примера, которые мы привели ранее:
1: водило неподвижно, солнце — это вход, а зубчатый венец — это выход.
Передаточное число (x+y)/[(x-D солнце /D Кольцо )y]
Но водило не движется, и его движение = x. Следовательно, х=0
Передаточное число становится y/[(-D sun /D Ring )y]
Или просто -D Ring /D Sun , что соответствует тому, что мы получили ранее.
2: Зубчатый венец удерживается неподвижно, солнце является входом, а водило планетарной передачи — выходом.Передаточное число равно (x+y)/x
Но зубчатый венец не движется, поэтому x-(D солнце /D Кольцо )y = 0, и y=x/(D солнце /D Кольцо )
Таким образом, наше передаточное отношение становится x[1+1/(D солнце /D кольцо )]/x или просто 1+(D кольцо /D солнце ).
Последний шаг, чтобы получить его в тех же терминах, что и раньше, состоит в том, чтобы понять, что диаметр носителя равен диаметру планеты плюс солнце (диаметр охватывает солнце плюс половина планеты на каждом конце), в то время как диаметр кольца — это диаметр двух планет плюс солнце (диаметр охватывает солнце и полную планету на обоих концах).
Передаточное число может быть выражено: D солнце /D солнце +(D Кольцо/ /D солнце ) или (D солнце +D Кольцо )/D солнце
Что тогда становится (D водила -D планета +D водила +D планета )/D солнце или 2*D держатель /D sun , термин, который мы получили ранее.
Техника суперпозиции позволяет гораздо легче анализировать более сложные планетарные устройства, и мы вернемся к ней чуть позже.
Двухступенчатые планетарные передачи
Типичная многоступенчатая планетарная передача представляет собой просто две или более стандартных планетарных передачи, соединенных последовательно. Например, если бы у вас во всех случаях были фиксированные кольца, ваше первое солнце было входом, а первое водило планетарной передачи подавалось на второе солнце, которое приводило в движение второе водило планетарной передачи в качестве выхода, ваше общее передаточное число было бы уменьшением вашего первый этап умножает на сокращение вашего второго.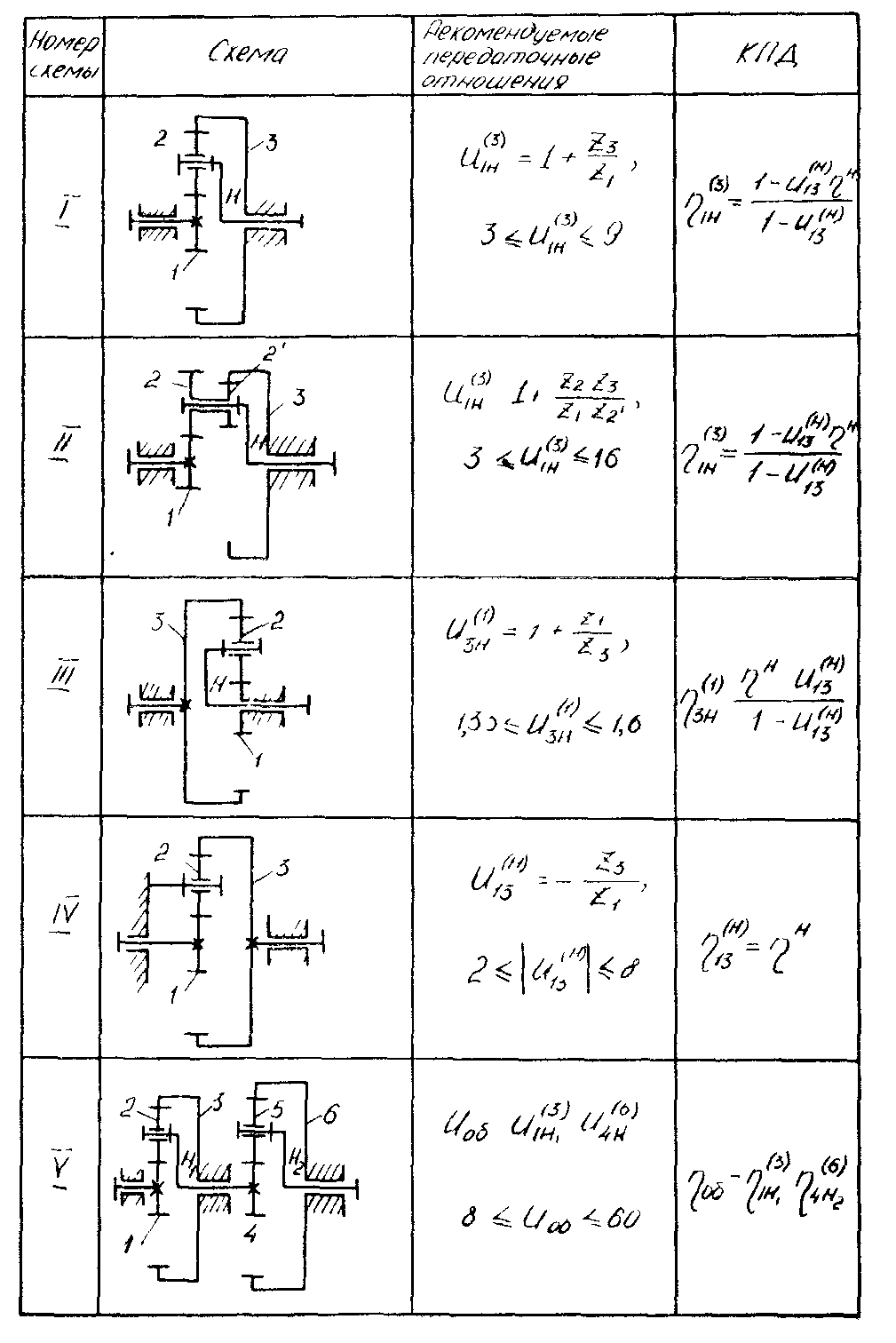
Это будет (1+(D Ring1 /D sun1 )*(1+(D Ring2 /D sun2 ).
Допустим, вы стремились к максимально возможному передаточному числу, ваше самое большое приемлемое зубчатое колесо имело 100 зубьев, и у вашего наименьшего приемлемого солнца было бы 12 зубьев, ваше самое большое двухступенчатое уменьшение было бы 87,1 к 1.
Дифференциальные планетарные передачи
Но что, если бы вы не просто расположили свои шестерни последовательно? три входа/выхода, что, если ваша первая ступень управляет двумя входами вашей второй ступени, вместо того, чтобы фиксировать что-либо во второй ступени? Такое расположение дает «дифференциальный планетарный» набор, где выход вашей второй ступени является функцией дифференциала между два входа Это похоже на дифференциал в вашем автомобиле, где скорость каждого колеса является функцией дифференциала между входом от карданного вала и другого колеса.0003
Одно из таких устройств показано на рисунке.
Сателлиты в обеих ступенях жестко закреплены между собой, первое кольцо неподвижно, общее водило планетарной передачи является входным, а второе кольцо — выходным.
Таблица наложения для этого расположения:
| Планеты | Кольцо 1 | Планетоноситель | Зубчатый венец 2 | |
| Только движущийся перевозчик | х | х | х | х |
| Неподвижная тележка | г | -(D Planet1 /D Ring1 )y | 0 | -(D Planet2 /D Ring2 )y |
| Общее движение | х+у | x -(D Планета1 /D Кольцо1 )y | х | x -(D Планета2 /D Кольцо2 )y |
Поскольку Кольцо 1 фиксировано, x -(D Планета 1 /D Кольцо 1 )y = 0, или y=(D Кольцо 1 /D 9006 2 Планета1 )x
Передаточное число — это скорость Носителя, деленная на Кольцо 2, или:
x/( x -(D Planet2 /D Ring2 )y) или 1/[1-(D Планета2 *D Кольцо1 )/(D Кольцо2 *D Планета1 )]
Чем ближе (D Планета2 *D Кольцо1 ) доходит до (D 9 0062 Кольцо2 *D Планета1 ) , тем выше будет ваше передаточное число (потому что знаменатель стремится к 0).
Если они на самом деле равны, передаточное число будет неопределенным, и, практически, ваш выход просто не будет двигаться вообще, поэтому нам нужна какая-то разница. Поскольку все планеты имеют общий центр, на каждый зуб, который вы добавляете к планете, кольцо на этой стадии будет увеличиваться на 1/2 зуба с каждой стороны, поэтому размеры планет и кольца изменяются в соотношении 1:1, получая больше или меньше вместе.
Теперь, если вы хотите, чтобы ваши силы были сбалансированы, вам нужно как минимум 2 планеты, каждая из которых должна быть меньше половины диаметра зубчатого венца. Допустим, у вашего самого большого приемлемого зубчатого венца 100 зубьев, а у вашей самой большой приемлемой планетарной передачи 45 зубов, максимальное возможное уменьшение (при условии, что все ваши шестерни имеют один и тот же модуль — используя разные модули на двух ступенях, можно достичь более высоких передаточных чисел) будет 1/[1-(44*100)/(45*99)] = 81 к 1. Хотя это неплохо, это хуже, чем простое последовательное расположение, о котором мы упоминали ранее.
Однако, если вы освободите место для солнца, таблица станет:
| Вс | Планеты | Кольцо 1 | Планетодержатель | Зубчатый венец 2 | |
| Только движущийся перевозчик | х | х | х | х | х |
| Перевозчик неподвижен | г | -(Dsun/Dplanet1)y | -(Dsun/D Ring1 )y | 0 | -(Dplanet2/D Ring2 )(Dsun/Dplanet1)y |
| Общее движение | х+у | х-(Dsun/Dplanet1)y | х -(Dsun/DRing1)y | х | x -(Dplanet2/DRing2)(Dsun/Dplanet1)y |
Позвольте вам посчитать, но если у вас есть шестерни следующих размеров:
- Солнце: 12 зубьев
- Планета 1: 44 зубца
- Кольцо 1: 100 зубьев
- Планета 2: 43 зубца
- Кольцо 2: 99 зубьев
вы получите отношение 726 к 1 .
Есть способы поиграть с профилем шестерни, чтобы получить число еще выше.
В качестве альтернативы, если вам не важны сбалансированные силы, и вы хотите обойтись без солнца, используйте следующие размеры шестерни:
- Планета 1: 90 зубьев
- Кольцо 1: 100 зубьев
- Планета 2: 89 зубов
- Кольцо 2: 99 зубьев
передаточное число поднимается еще выше, до 891 к 1.
Один из способов понять, почему работает такое расположение шестерен, — представить два набора сателлитов с одинаковым числом зубьев. Каждый раз, когда сателлиты продвигаются вперед на один зуб, два набора зубчатых колес выравниваются по зацепляющемуся зубу. Если бы зубчатые венцы также имели одинаковое количество зубьев, они совпадали бы по каждому зубу, а поскольку один из них зафиксирован, другой тоже не двигался бы. Однако, поскольку неподвижная шестерня имеет один дополнительный зуб, каждый раз, когда сателлиты совершают полный оборот вокруг неподвижной шестерни, подвижная зубчатая передача отстает на один зуб.
Чтобы отстать от всего оборота и, таким образом, выходной сигнал сместился на один оборот, сателлиты должны были бы сделать количество полных оборотов вокруг зубчатого венца, равное количеству зубьев в подвижном зубчатом венце. Если вы знакомы с гармоническими передачами, они работают примерно так же.
Почти так и есть, за исключением того, что у сателлитов тоже нет зуба, поэтому количество зубьев, на которые выходной сигнал отстает от неподвижной шестерни, немного отличается. В нашем первом случае 45-зубчатая шестерня поворачивается примерно 2,22 раза каждый раз, когда она проходит вокруг 100-зубчатой коронной шестерни, которая поворачивает 44-зубую шестерню примерно на 97,78 зубьев. Таким образом, выходная шестерня с 99 зубьями перемещается примерно на 1,22 зуба (99–97,78) каждый раз, когда сателлиты совершают полный оборот. 99/1,22 = 81 плюс ошибка округления, которая является передаточным числом, которое мы получили ранее.
Есть практические проблемы с этим расположением передач.
Одной из таких проблем является низкий КПД. В типичном прямозубом или косозубом зубчатом механизме некоторые шестерни передают низкий крутящий момент, но вращаются быстро, а некоторые шестерни передают высокий крутящий момент, но движутся медленно. Это обеспечивает относительно низкие потери энергии. Однако в этом случае сателлиты входят в зацепление с выходной шестерней, что влечет за собой высокие нагрузки, а также быстрое движение.
На примере, где на входе было водило планетарной передачи, на выходе — вторая зубчатая передача, а шестерни имели следующие размеры:
- Планета 1: 45 зубьев
- Кольцо 1: 100 зубьев
- Планета 2: 45 зубьев
- Кольцо 2: 99 зубьев
Если входная скорость составляет 100 об/мин, выходная скорость составляет всего 1,2 об/мин, но планеты вращаются со скоростью более 200 об/мин, хотя напрямую связаны с выходной. Сочетание высоких сил скольжения и большого количества движений приводит к потере большого количества энергии.
Однако есть еще один способ понять, почему эта шестеренка работает, и это состоит в том, чтобы думать о стадиях как о двух отдельных планетарных механизмах. Для любого конкретного расположения, если вы установите два ваших входа/выхода, будет определен третий. Например, в расположении выше, с двумя наборами зубчатых колес и водилом (входным), которое несет два набора сателлитов, соединенных вместе, поскольку вы фиксируете одно зубчатое колесо, если во втором наборе шестерни точно такие же. размера, при том же входе (в данном случае водила) второй зубчатый венец не двигался. Это потому, что у него будет такое же отношение зубчатого венца к другим зубчатым колесам, как и в первом наборе, и, поскольку все остальное движется точно так же, второе зубчатое колесо будет двигаться так же, как и первое, то есть не совсем. Если два этапа почти идентично, но не совсем, второй зубчатый венец будет почти неподвижным, что дает вам высокое передаточное число.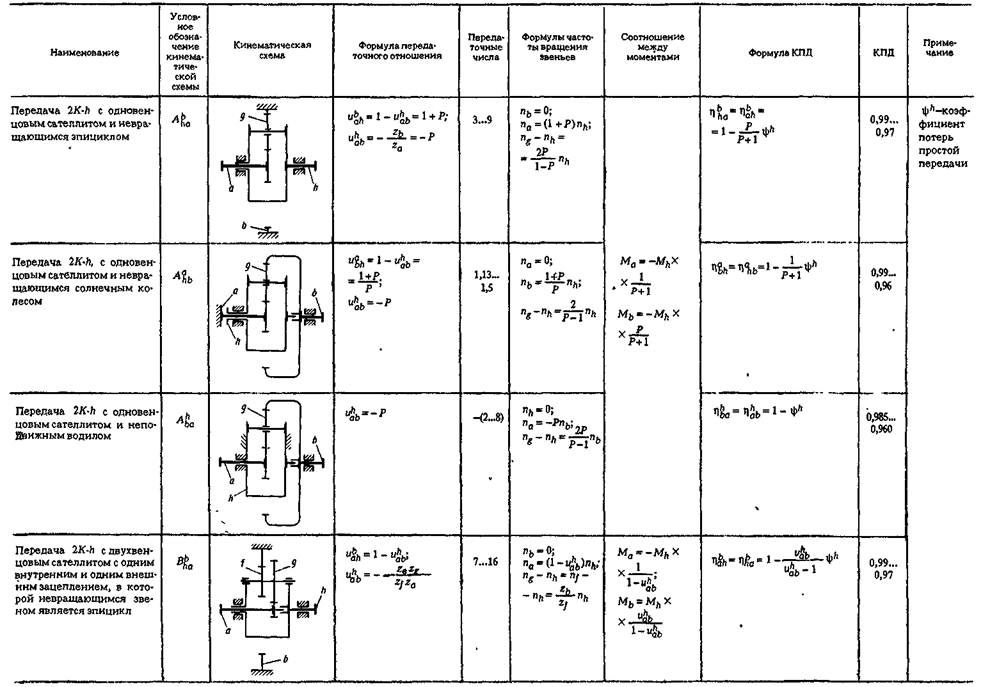
Если вы думаете об этом таким образом, это открывает двери для рассмотрения других механизмов шестерен, где у вас есть две почти идентичные ступени, фиксируете компонент одной и используете эквивалент во второй ступени в качестве выходных данных. Рассмотрим одну такую схему в качестве последнего примера этой статьи.
Солнца двух ступеней будут вращаться вместе, и два зубчатых венца тоже будут вращаться вместе. Несущая первой ступени фиксирована, а выходной является носитель второй ступени.
Рис.7: Дифференциал Планетарная передача 2Используя общую таблицу для планетарной передачи, полученную ранее, таблица, представляющая каждую ступень:
И:
| Этап 2 | Вс | Планета | Планетодержатель | Зубчатый венец |
| Только движущийся перевозчик | Х2 | Х2 | Х2 | Х2 |
| Неподвижная тележка | Y2 | -(Dsun2/DPlanet2)y2 | 0 | -(Dsun2/DRing2)y2 |
| Общее движение | X 2 +y 2 | X 2 -(Dsun 2 9 0304 /DPlanet 2 ) y2 | Х 2 | X 2 -(Dsun 2 /DRing 2 ) у2 |
Первый этап — это схема, с которой мы знакомы.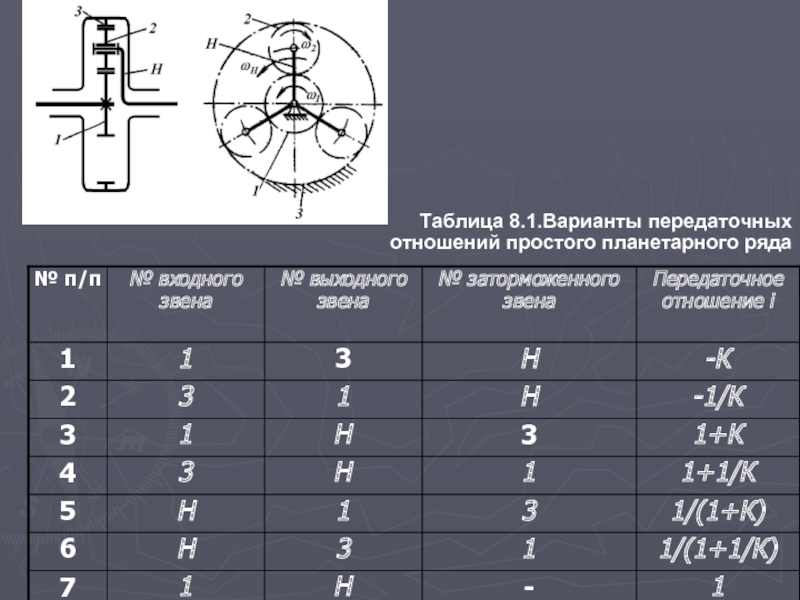
Мы уже определили, что соотношение скоростей зубчатого венца и солнечной шестерни будет следующим:
(-Dsun1/Dring1):1
Это дает нам ряд уравнений для работы.
Поскольку первое водило неподвижно:
1) x1=0
Поскольку солнечные шестерни имеют общий вал, они вращаются с одинаковой скоростью, таким образом:
(x1+y1)=(x2+y2), что становится
2) y1=(x2+y2) потому что x1=0
Поскольку зубчатые венцы вращаются вместе, и с использованием уже известного отношения зубчатого венца к солнцу:
x 2 9006 1 -(D солнце 2 /D Кольцо 2 9 0305 ) y 2 = 9 0305 ( -D солнце1 /D кольцо1 )(x 1 +y 1 ) <- но x 1 = 0, поэтому
x 903 04 2 -(Д солнце 2 /D Кольцо 90 063 2 ) у 2 903 05 = (-D солнце1 /D кольцо1 )(y 1 ) или
3) y 1 = [ 9 0304 ((Д солнце 2 /D Кольцо 903 04 2 ) у 2 9030 4 – x 2 ]/( D солнце1 /D кольцо1 )
Приравнивание y1 к 2 ) и 3) дает:
(x 2 +y 2 ) = у 2 [( D солнце 2* D кольцо1 ) / ( D Кольцо 2 * D солнце1 )] – x 2 ( D Кольцо 1 / D солнце 1 9 0066 )
x 2 (1+ D Кольцо 1 / D солнце 90 304 1 ) = y 2 [( D солнце 2* D кольцо1 ) 9030 4 / ( D Кольцо 2 * D солнце1 ) – 1]
4) у 2 = х 2 90 063 {(1+ Д Кольцо 1 / D солнце 903 04 1 )/ [( D солнце 900 62 2* D кольцо1 ) / ( D 90 061 Кольцо 2 * D sun1 ) – 1]}
Передаточное число:
(x 2 +y 90 062 2 )/x 2
На основе на 4) получается:
1+{(1+ D Кольцо 1 9 0066 / D солнце 1 )/ [( D солнце 2* 9006 3 D кольцо1 ) / ( D Кольцо 2 * D вс1 ) – 1]}
После некоторой перестановки получается:
D кольцо1 (D солнце2 +D кольцо2 )/[(D солнце2 *D кольцо1 )-(D солнце1 *D кольцо2 )]
беспорядок, но если мы просто рассмотрим знаменатель, передаточное число будет максимальным, когда (D солнце2 *D кольцо1 ) максимально близко к (D солнце1 *D кольцо2 ), но не будет точно равным (что означало бы, что водило на этапе 2 будет двигаться ровно столько же, сколько носитель на этапе 1, то есть совсем не будет).