Как измерять крутящий момент? | Dewesoft
Автор: Грант Малой Смит (Grant Maloy Smith), специалист по сбору данных
Данная статья об измерении крутящего момента поможет вам:
- Понять, что такое крутящий момент
- Узнать, как измерять крутящий момент
- Ознакомиться со спецификой измерения крутящего момента при сборе данных
Что такое крутящий момент?
Если вы не пропускали уроки физики в школе, то помните, что сила — это воздействие, приводящее тело в движение в течение времени. Например, простое линейное усилие может толкнуть (или притянуть) массу в состоянии покоя и изменить её скорость путём ускорения. Крутящий момент — сила, которая вызывает вращение тела по своей оси вращения. Так, крутящий момент — это крутящее усилие, которое называют вращающей силой.
Наиболее очевидный пример крутящего момента — приводной вал автомобиля.
Вызываемый двигателем крутящий момент вала приводит автомобиль в движение. Крутящий момент — это вектор: это означает, что он имеет направление.
Крутящий момент — усилие, вращающее или поворачивающее приводной вал, винт или колесо.
Вращающее усилие
Также крутящий момент называют моментом или моментом силы. Как правило, крутящий момент обозначают символом $τ$ (греческой буквой «т»). Единица измерения крутящего момента по системе СИ — $N\cdot m$ (Н·м).
В США для его выражения используют футо-фунты ($ft/lbs$). Для перевода $N\cdot m$ в $ft/lbs$ достаточно разделить $N\cdot m$ на 1,356.
Старшина второй статьи Джеймс Р. Эванс (James R. Evans) осматривает приводной вал хвостового винта вертолёта ВМС США. Снимок из открытого доступа, Wikimedia Commons
Для чего измеряют крутящий момент?
Измерение механического крутящего момента торсионных валов — важнейший этап проектирования и сбора различных машин, а также устранения их неисправностей.
Истинное значение механического крутящего момента вала, пропеллера или другого вращающегося компонента — единственный способ понять, отвечает ли он требованиям.
В некоторых случаях крутящий момент необходимо отслеживать постоянно: например, чтобы предотвратить потенциально опасный чрезмерный крутящий момент, который может привести к выходу системы из строя. Также измерения крутящего момента играют важную роль при диагностическом техническом обслуживании.
Какие виды крутящего момента существуют?
Крутящий момент делится на два вида: вращающий и реактивный:
- вращающий — то есть вращающий или динамический крутящий момент;
- реактивный — то есть стационарный или статичный крутящий момент.
Вращающий момент
Тела, которые многократно (или постоянно) вращаются вокруг своей оси (например, валы, турбины, колёса), имеют вращающий момент.
Реактивный момент
Воздействующая на тело статичная сила называется реактивным крутящим моментом.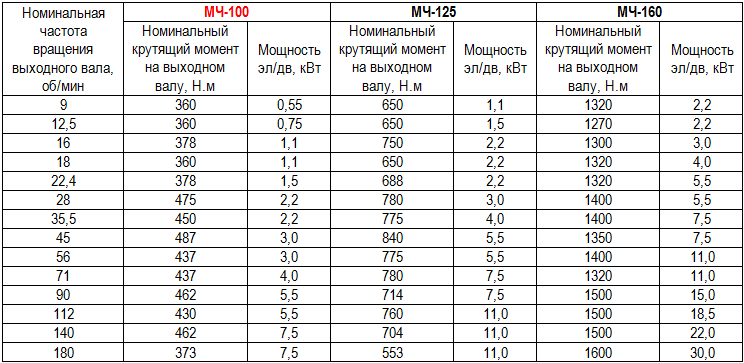
Например, при попытке закрутить болт ключом на болт воздействует реактивная сила. Такая сила воздействует даже тогда, когда болт не крутится. В таких случаях крутящий момент измеряют не за полный оборот.
Как измеряется крутящий момент?
Крутящий момент можно измерить косвенно или напрямую. Если известны КПД двигателя и скорость вала, с помощью измерителя мощности можно вычислить крутящий момент. Такое измерение называют косвенным.
Более точным методом является прямое измерение крутящего момента с помощью датчиков крутящего момента или роторных моментомеров. Чем они отличаются?
Датчики реактивного (статичного) крутящего момента
Датчик Torquemaster. CC BY-SA 3.0, Wikimedia Commons
Датчик реактивного крутящего момента измеряет статический крутящий момент.
Пример датчика крутящего момента — динамометрический ключ. С помощью таких ключей можно точно измерить крутящий момент, прилагаемый к болту, гайке или другому креплению.
В основании ключа можно задать нужный крутящий момент, после чего при затягивании крепления оператором до нужного момента раздастся щелчок. Как правило, такие ключи называют щелчковыми. На них можно задать несколько значений момента.
Цифровые динамометрические ключи оснащены иглой или цифровым дисплеем, на котором отображается прилагаемое усилие. Ряд электронных моделей (в частотности промышленных) имеют память, в которой хранится каждое измерение значение (для ведения документации или контроля качества).
Принцип работы щелчкового динамометрического ключа продемонстрирован в следующем видео:
В основе датчика реактивного крутящего момента лежит кварцевый пьезоэлектрический датчик или тензодатчик. Сегодня на рынке представлены различные виды и конфигурации динамометрических ключей и отвёрток.
Датчики крутящего момента
Датчик крутящего момента — это преобразователь, который преобразовывает вращающий момент в сигнал, который можно измерить, проанализировать, отобразить и сохранить.
Преобразователи крутящего момента применяются для испытаний крутящего момента двигателя, испытаний ДВС, испытаний электродвигателей, валов, турбин, генераторов и т.д.
Измерить крутящий момент можно как напрямую, так и косвенно.
Косвенное измерение крутящего момента — более экономичный и удобный метод измерения, точность которого уступает методу прямого измерения. Он подходит для случаев, когда известен КПД двигателя и имеется возможность измерить скорость вала и расход тока.
Прямое измерение — более точный способ. Для прямого измерения на вале закрепляют тензодатчик, который измеряет крутящее усилие на вале.
На вале закрепляют тензодатчик. Вращательное усилие заставляет вал вращаться.
При повороте вала двигателем вращательное усилие будет незначительным. Из-за жёсткости стали увидеть вращение нельзя, однако его можно считать с помощью закреплённых на вале тензодатчиков. Четыре датчика образуют мост Уитстона, выход которого балансируется и нормируется системой измерения крутящего момента.
Выход тензодатчика можно передать по проводу (если возможно) или дистанционно на систему измерения крутящего момента или систему сбора данных.
Стандартная система измерения крутящего момента
Внутри датчика крутящего момента выходы закреплённых на вале тензодатчиков передаются на электронные компоненты по контактному кольцу (на тензодатчики должно подаваться питание). Также можно подключить бесщёточный или индуктивный датчик: он повышает скорость и меньше изнашивается, а значит требует меньшего технического обслуживания. Бесконтактным способом можно измерить угол и частоту вращения.
Системы сбора данных Dewesoft — идеальные решения для измерения любых физических параметров, в том числе крутящего момента. В них встроены изолированные блоки преобразования сигналов, которые сокращают количество шумов и гарантируют высокую точность данных. Также они имеют входы счётчика, частоты вращения и энкодера, а значит подходят для одновременного измерения скорости, угла и положения вала.
В системах сбора данных данные с аналоговых и цифровых счётчиков полностью синхронизированы между собой, и этот фактор играет важную роль при решении любых задач, особенно при испытании вибрации кручения и вращения. Подробнее об этом — в следующем разделе.
Испытание вибрации кручения и вращения в ПО Dewesoft X
Стационарные системы измерения крутящего момента
В представленной выше системе датчик крутящего момента закреплён между двигателем и тормозом с помощью соединений с каждой стороны. Проходящий через вал датчик оснащен тензодатчиком, который измеряет крутящее усилие вала. После преобразования выход сигнала отправляется на систему сбора данных, цифровой дисплей или аварийную систему (при мониторинге, а не записи данных).
При необходимости датчики крутящего момента можно оснастить энкодером, который точно выводит скорость и угол вала. Такие выводы применяют для анализа вибрации кручения и вращения. Выводы скорости и угла крайне важны при использовании динамометров для вычисления выходной мощности (выраженной в $HP$ или $Kw$) и КПД двигателя.
Портативные системы измерения крутящего момента
Для временных измерений крутящего момента тензодатчики можно закрепить на приводном вале. Компактный интерфейс с питанием от аккумулятора питает датчики и дистанционно передаёт данные на ближайший блок преобразования, в котором с помощью системы сбора данных их можно записать, отобразить или проанализировать.
Беспроводной датчик крутящего момента. Изображение предоставлено компанией Parker-LORD MicroStrain Sensing
Беспроводные датчики Parker-Lord совместимы с ПО Dewesoft X: их можно объединить с системами сбора данных и использовать на неограниченном количестве каналов.
Области применения порядкового анализа
Вибрации кручения могут стать причиной выхода торсионных валов из строя. Анализ вибрации вращения и кручения — важный способ устранения неисправностей валов, коленчатых валов и зубчатых передач в автомобилестроении, промышленности и в производстве электроэнергии.
Что такое вибрация кручения?
Вибрации кручения — угловые вибрации тела (как правило, вала по оси вращения).
Данные механических вибраций вызваны изменениями крутящего момента с течением времени, наложенными на постоянную скорость торсионного вала. В автомобилестроении основной причиной вибраций кручения становятся колебания полезной мощности двигателя.
Вибрации кручения оценивают как изменение скорости вращения в цикле вращения. Изменения частоты вращения обусловлены нестабильным крутящим моментом или переменной нагрузкой.
Что такое вибрация вращения?
Вибрация вращения — динамическая составляющая скорости вращения. При точном измерении вибрации вращения вала в некоторых участках разгона можно увидеть сильное отклонение скорости вращения. Отклонение возникает в результате угловой вибрации, пересекающей собственную угловую частоту вала. Угловая вибрация вычисляется путём отсечения постоянной составляющей скорости или угла вращения;
Вибрация кручения зависит от ряда параметров: свойств материала и условий эксплуатации (температуры, нагрузки, частоты вращения и т.д.).
Как измерять вибрацию вращения и кручения
В этом коротком видео показаны способы измерения вибрации и вращения, а также описана базовая теория и практические преимущества таких измерений.
Модуль вибрации кручения Dewesoft X автоматически вычисляет следующие параметры:
- угол поворота: фильтрованное значение угла вибрации;
- скорость вращения: фильтрованное значение скорости вибрации;
- угол кручения: динамический угол кручения, который представляет собой разность углов, полученных от датчика 1 и датчика 2;
- скорость кручения: разница угловых скоростей, полученных от датчика 1 и датчика 2;
- опорный угол по оси X: опорный угол, который всегда составляет от 0 до 360° и может быть использован в качестве опорного на графике XY;
- частота: об/мин.
Вычисления можно провести в ходе измерения, а также на этапе обработки (по необработанным данным).
Итог
Датчики крутящего момента применяются для решения сотен задач во всех отраслях. Датчики реактивного крутящего момента применяются в динамометрических ключах и других инструментах.
В автомобилестроении датчики крутящего момента устанавливают в стойки испытания двигателей, динамометры, испытательные стенды, а также стенды испытаний на долговечность. Но это лишь базовые применения, помимо которых датчики применяют для испытания промышленных установок кондиционирования воздуха, крупномасштабных кормушек для животных и птиц, робототехники, монтажного и медицинского оборудования, электрооборудования и т.д.
Крутящий момент — важный параметр в множестве отраслей. К счастью, его можно измерить с помощью датчиков и преобразователей, и отобразить, записать и проанализировать с помощью систем сбора данных.
Поделиться статьёй:
Крутящий момент | это… Что такое Крутящий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Содержание
|
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы.
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в. м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
- Момент инерции
- Момент импульса
- Теорема Вариньона
Преобразование единиц измерения крутящего момента
Преобразование значений крутящего момента и единиц измерения в соответствии с вашими потребностями!
«Сколько Нм составляют 12,7 фут-фунта?»
Страница преобразования крутящего момента немедленно выполняет для вас
преобразований! Значения во всех общепринятых единицах измерения крутящего момента могут быть немедленно преобразованы в другие распространенные единицы измерения крутящего момента.
Найдите исходную единицу измерения и введите исходное значение, чтобы преобразовать значения крутящего момента в другие единицы измерения.
дюйм-грамм
| Блок | Значение |
|---|---|
| Дюйм-грамм | |
| Дюймы Фунты | |
| Миллиньютон-метры | |
| Сенти Ньютон Метры | |
| Деци Ньютон Метры | |
| Ньютон-метры | |
| Килограмм Сантиметров |
дюймовых унций
| Блок | Значение |
|---|---|
| Дюймовые унции | |
| Дюйм-грамм | |
| Дюймы Фунты | |
| Фунты Фунты | |
| Миллиньютон-метры | |
| Сенти Ньютон Метры | |
| Деци Ньютон Метры | |
| Ньютон-метры | |
| Грамм Сантиметры | |
| Килограмм Сантиметры | |
| Килограммы |
дюйма фунта
| Блок | Значение |
|---|---|
| Дюймы Фунты | |
| Дюйм-грамм | |
| Дюймовые унции | |
| Фунты Фунты | |
| Миллиньютон-метры | |
| Сенти Ньютон Метры | |
| Деци Ньютон Метры | |
| Ньютон-метры | |
| Килограмм Сантиметры | |
| Килограммы |
футо-фунта
| Блок | Значение |
|---|---|
| Фунт-фунт | |
| Дюйм-грамм | |
| Дюймовые унции | |
| Дюймы Фунты | |
| Миллиньютон-метры | |
| Сенти Ньютон Метры | |
| Деци Ньютон Метры | |
| Ньютон-метры | |
| Килограмм Сантиметры | |
| Килограммы |
миллиньютон-метра
| Блок | Значение |
|---|---|
| Миллиньютон-метры | |
| Дюйм-грамм | |
| Дюймовые унции | |
| Дюймы Фунты | |
| Фунты Фунты | |
| Сенти Ньютон Метры | |
| Деци Ньютон Метры | |
| Ньютон-метры | |
| Килограмм Сантиметры | |
| Килограммы | |
| Грамметры |
санти ньютон метры
| Блок | Значение |
|---|---|
| Санти Ньютон Метры | |
| Дюйм-грамм | |
| Унции в дюймах | |
| Дюймы Фунты | |
| Фунты Фунты | |
| Миллиньютон-метры | |
| Деци Ньютон Метры | |
| Ньютон-метры | |
| Килограмм Сантиметры | |
| Килограммы | |
| Грамм Сантиметр |
Деци Ньютон Метров
| Блок | Значение |
|---|---|
| Деци Ньютон Метры | |
| Дюйм-грамм | |
| Дюймовые унции | |
| Дюймы Фунты | |
| Фунты Фунты | |
| Миллиньютон-метры | |
| Сенти Ньютон Метры | |
| Ньютон-метры | |
| Килограмм Сантиметры | |
| Килограммы |
ньютон-метра
| Блок | Значение |
|---|---|
| Ньютон-метры | |
| Дюйм-грамм | |
| Дюймовые унции | |
| Дюймы Фунты | |
| Фунты Фунты | |
| Миллиньютон-метры | |
| Сенти Ньютон Метры | |
| Деци Ньютон Метры | |
| Килограмм Сантиметров | |
| Килограммы |
Килограмм Сантиметров
| Блок | Значение |
|---|---|
| Килограмм Сантиметры | |
| Дюйм-грамм | |
| Дюймовые унции | |
| Дюймы Фунты | |
| Фут Фунт | |
| Миллиньютон-метры | |
| Сенти Ньютон Метры | |
| Деци Ньютон Метры | |
| Ньютон Сантиметры |
килограмма метров
| Блок | Значение |
|---|---|
| Килограммы | |
| Унции в дюймах | |
| Дюймы Фунты | |
| Фунты Фунты | |
| Миллиньютон-метры | |
| Сенти Ньютон Метры | |
| Деци Ньютон Метры | |
| Ньютон-метры | |
| Килограмм Сантиметры |
Характеристики крутящего момента и концепции | Park Tool
25 августа 2015 г. /
Разное Темы
В этой статье обсуждаются основы использования динамометрического ключа и динамометрического ключа. См. также соответствующую статью об основных понятиях потоков. Эта статья включает в себя таблицу с различными рекомендациями по крутящему моменту.
1
Введение в Torque
Резьбовые крепления, такие как гайки и болты, используются для крепления многих компонентов велосипеда. Когда застежка затягивается, застежка фактически изгибается и растягивается, подобно резиновой ленте. Это растяжение не является постоянным, но оно дает суставной силе удерживать вместе, что называется «предварительной нагрузкой» или напряжением. Каждое крепление рассчитано на определенный диапазон натяжения. Слишком сильное затягивание приведет к деформации резьбы или деталей. Слишком маленькая предварительная нагрузка будет означать, что застежка ослабнет при использовании. Это может привести к повреждению компонентов, таких как кривошип с ослабленным крепежным болтом. Ослабленные болты и гайки также обычно являются источником различных скрипов на велосипеде.
Натяжение застежки во многом зависит от величины крутящего момента, степени затяжки и размера резьбы. Как правило, инженеры указывают размер резьбы, достаточно большой, чтобы выдерживать ожидаемые нагрузки. Например, болт M5 сепаратора бутылки с водой не будет хорошим выбором для удержания рукоятки. Даже если бы болт был максимально затянут, его силы не хватило бы для надежной фиксации рычага на шпинделе. Интерфейс кривошип-шпиндель подвергается довольно большой нагрузке, что делает более крупные резьбы (M8, M12, M14) лучшим выбором. Величина давления, прилагаемого резьбой, может быть существенной, чтобы надежно удерживать соединение. Например, полностью затянутый болт кривошипа может обеспечить усилие более 14 000 ньютонов (сила 3000 фунтов), поскольку он удерживает рычаг на месте.
Принято считать, что болты и гайки часто откручиваются «само по себе», без видимой причины. Однако распространенной причиной ослабления резьбовых соединений является просто отсутствие натяжения при первоначальной сборке. Вибрация, нагрузка, использование или неправильное обращение обычно не могут преодолеть силу зажима в правильно подобранном и надежном резьбовом креплении. Согласно простому эмпирическому правилу, любой крепеж должен быть затянут как можно туже без повреждения резьбы или составных частей. Это означает, что самая слабая часть сустава определяет пределы напряжения и, следовательно, крутящего момента.
2
Измерение крутящего момента
Крутящий момент для механиков — это просто крутящее или вращательное движение вокруг оси резьбы. Это сопротивление может быть соотнесено с натяжением крепежа, но не является его прямым измерением. Как правило, чем выше сопротивление вращению, тем больше натяжение в резьбовом креплении. Другими словами, чем больше усилий требуется, чтобы затянуть болт, тем сильнее он затянут.
Крутящий момент измеряется как единица силы, действующей на вращающийся рычаг определенной длины. В велосипедной индустрии и других местах общепринятой единицей измерения крутящего момента является 9. 0664 Ньютон-метр (сокращенно Нм). Один ньютон-метр — это сила в один ньютон на рычаге длиной один метр. Другая единица измерения, которую иногда можно увидеть, — это килограмм-сантиметр (сокращенно кгс-см), который представляет собой килограмм силы, действующей на рычаг длиной один сантиметр. Можно конвертировать между различными системами.
В Соединенных Штатах также иногда используется дюйм-фунт (сокращенно in-lb). Это сила в один фунт, действующая на конец рычага (гаечного ключа) длиной в один дюйм. Другой единицей крутящего момента, используемой в США, является футо-фунт (сокращенно фут-фунт), который представляет собой силу в фунтах, воздействующую на рычаг длиной в один фут. Можно преобразовать между двумя единицами, умножив или разделив на двенадцать. Поскольку это может привести к путанице, лучше придерживаться одного обозначения. Единицы, указанные в таблице крутящего момента здесь, будут в дюйм-фунтах.
Возможно преобразование между различными системами:
- Нм = дюйм-фунт x 0,113
- Нм = фут-фунт x 1,356
- Нм = кг-см x 0,0981
3
Типы динамометрических ключей
Динамометрические ключи — это просто инструменты для измерения сопротивления вращению. Существует корреляция между натяжением болта и усилием, которое требуется для его поворота. Любой инструмент, даже динамометрический ключ, следует использовать со здравым смыслом. Болт с крестообразной резьбой не будет должным образом затянут даже динамометрическим ключом. Механик должен знать назначение крутящего момента, а также то, как крутящий момент и предварительная нагрузка крепежа влияют на соединение компонентов. Также важно учитывать подготовку резьбы, которая подробно рассмотрена в этой статье.
Балочный
Park Tool предлагает динамометрические ключи двух типов. Оба ключа используют квадратный хвостовик 3/8″ для установки стандартных бит 3/8″.
TW-1.2 имеет диапазон 0–14 Нм (0–140 дюйм-фунтов). TW-2.2 имеет диапазон 0–60 Нм (0–50 футо-фунтов).
Конструкция балки относительно проста и подходит как для левой, так и для правой резьбы. Головка с гнездом удерживает две стальные балки, основную балку и индикаторную или стрелочную балку. Первичный луч отклоняется при вытягивании рукоятки. Отдельный указательный луч остается неотклоненным, а основной луч под ним изгибается и перемещается вместе с рукояткой. Показания снимаются на конце указателя, на считывающей пластине на первичном луче. Ручка перемещается до тех пор, пока не будет достигнуто желаемое значение. Эти ключи редко требуют повторной калибровки. Если стрелка указателя не указывает на ноль, когда инструмент находится в состоянии покоя, она просто отгибается назад до тех пор, пока не выровняется. Усталость стали не проблема.
Щелчковый тип
Park Tool предлагает динамометрические ключи с защелкой двух типов. Оба ключа используют квадратный хвостовик 3/8″ для установки стандартных бит 3/8″.
Диапазон крутящего момента TW-5.2 составляет 2–14 Нм (18–124 дюйм-фунт). TW-6.2 имеет диапазон 10–60 Нм (88–530 дюймов-фунтов).
Термин «тип клика» может ввести в заблуждение. В данной конструкции динамометрических ключей используется поворотная головка. Есть пружина, которая сжимается при повороте рукоятки. При более высоких настройках пружина сжимается сильнее, что позволяет головке поворачиваться только при более высоком сопротивлении и более высоком крутящем моменте. При высокой настройке слышен щелчок. Но при более низких настройках шум может быть незначительным или вообще отсутствовать, поскольку головка перемещается при повороте. Поворот головки указывает на достижение сопротивления или крутящего момента, а не на щелчок.
4
Характеристики крутящего момента для велосипеда
Ниже приведена таблица эквивалентов крутящего момента, а формулы для преобразования следуют за таблицей крутящего момента. Таблица также доступна в виде файла PDF.
Все цифры в таблице ниже даны в ньютон-метрах и дюйм-фунтах. Обратите внимание, что некоторые компании не указывают крутящий момент для определенных компонентов или деталей. Свяжитесь с производителем для получения самых последних спецификаций.
Колесо, ступица, задняя шестерня Зона
| Компонент | Тип/марка | Ньютон-метры | Дюйм-фунты |
|---|---|---|---|
| Натяжение спицы | Крутящий момент обычно не используется в колесах. Натяжение спиц измеряется по прогибу. Обратитесь к производителю обода за конкретными рекомендациями по натяжению. См. ТМ-1. | ||
| Ось | Быстросъемный: закрытый кулачковый тип | Измеренный крутящий момент обычно не используется. Общепринятой отраслевой практикой является сопротивление рычага на полпути от открытого положения до полного закрытия. Дополнительную информацию см. в разделе «Снятие и установка шин и камер». | |
| Гайки сплошной оси (колеса небыстросъемного типа) | 29,4–44 | 266–390 | |
| Стопорное кольцо звездочки кассеты | Шимано® | 29,4–49 | 260–434 |
| СРАМ® | 40 | 354 | |
| Кампаньоло® | 50 | 442 | |
| Стопорная гайка конуса ступицы | Бонтрагер® | 17 | 150 |
Крис Кинг® | 12,2 | 100 | |
| Шимано® | 9,8–24,5 | 87–217 | |
| Корпус втулки | Бонтрагер® | 45 | 400 |
Shimano® | 35–50 | 305–434 | |
| Shimano® XTR с шестигранником 14 мм | 45–50 | 392–434 | |
Гарнитура, руль, сиденье и подседельный штырь
| Компонент | Тип/Марка | Ньютон-метры | Дюйм-фунты |
|---|---|---|---|
| Контргайка гарнитуры с резьбой | Зажимная гайка Chris King®, тип | 14,6–17 | 130–150 |
| Танге-Сейки® | 24,5 | 217 | |
| Болт крепления штока: пинольный для резьбовых гарнитур | Шимано® | 19,6–29,4 | 174–260 |
| Общий ассортимент | 16-18 | 144–168 | |
| Болты крепления рулевой колонки без резьбы | Деда® | 8 | 71 |
| Углерод FSA® | 8,8 | 78 | |
| Шплинт Syncros®, тип | 10,1 | 90 | |
| Томсон® | 5,4 | 48 | |
| Монолинк Time® | 5 | 48 | |
| Race Face® | 6,2 | 55 | |
| Крепление выноса руля: 1 или 2 болта крепления | Шимано® | 19,6–29,4 | 174–260 |
| Control Tech® | 13,6–16,3 | 120–144 | |
| Крепление выноса руля: лицевая панель с 4 болтами | Контрольная технология® | 13,6–16,3 | 120–144 |
| Deda® магний | 8 | 71 | |
| FSA® OS-115 углерод | 8,8 | 78 | |
| Race Face® | 6,2 | 55 | |
| Томсон® | 5,4 | 48 | |
| Монолинк Time® | 6 | 53 | |
| Удлинители руля MTB | Кейн Крик® | 7,9 | 70 |
| Control Tech® | 16,3 | 144 | |
| Крепление для направляющих сиденья | Шимано® | 20–30 | 174–260 |
| Кампаньоло® | 22 | 194 | |
| Control Tech® с двумя болтами | 16,3 | 144 | |
| Control Tech® с одним болтом, тип | 33,9 | 300 | |
| Синкрос® | по 5 болтов | 44,2 болта | |
| Монолинк Time® | 5 | 44,2 | |
| Труватив® | Болт M8: 22–24 Болт M6: 6–7,1 | Болт M8: 195–212 Болт M6: 53–63 | |
| Держатель стойки сиденья* | Кампаньоло® | 4–6,8 | 36–60 |
*ПРИМЕЧАНИЕ: Стойки сиденья требуют лишь минимального затягивания, чтобы не соскользнуть вниз. Избегайте чрезмерного затягивания.
Система шатунов, каретка и область педалей
| Компонент | Тип/марка | Ньютон-метры | Дюйм-фунты |
|---|---|---|---|
| Педаль в кривошип | Шимано® | 35 минимум | 309,7 минимум |
| Кампаньоло® | 40 | 354 | |
| Ричи® | 34,7 | 307 | |
| Труватив® | 31,2–33,9 | 276–300 | |
| Стяжные болты кривошипа со шлицем | Shimano® Hollowtech® II | 9,9–14,9 | 88–132 |
| FSA® MegaExo™ | 9,8–11,3 | 87–100 | |
| Колпачок регулировки кривошипа | Shimano® Hollowtech® II | 0,5–0,7 | 4–6 |
| FSA® MegaExo™ | 0,5–0,7 | 4–6 | |
| Болт шатуна (включая шатуны со шлицами и шатуны с квадратным валом) | Шимано® | 34–44 | 305–391 |
| Shimano® Octalink® XTR® (резьба M15) | 40,3–49 | 357–435 | |
| Кампаньоло® | 32–38 | 282–336 | |
| Кампаньоло® Ultra-Torque® | 42 | 371 | |
| Болт FSA® M8 | 34–39 | 304–347 | |
| Сталь FSA® M14 | 49–59 | 434–521 | |
| Race Face® | 54 | 480 | |
| Синкрос® | 27 | 240 | |
| Truvativ® ISIS Drive | 43–47 | 384–420 | |
| Квадратный стержень Truvativ® | 38–42 | 336–372 | |
| Уайт Индастриз™ | 27–34 | 240–300 | |
| Колпачок шатуна с одним ключом | Шимано® | 5–6,8 | 44–60 |
| Труватив® | 12–14 | 107–124 | |
| Кассета звездочки к шатуну (стопорное кольцо) | Шимано® | 50–70 | 443–620 |
| Болт звездочки: сталь | Шимано® | 7,9–10,7 | 70–95 |
| Кампаньоло® | 8 | 71 | |
| Race Face® | 11,3 | 100 | |
| Труватив® | 12. 1–14 | 107–124 | |
| Болт звездочки: алюминий | Шимано® | 5–10 | 44–88,5 |
| Кампаньоло® | 8 | 70,8 | |
| Труватив® | 8–9 | 70,8–79,6 | |
| Нижний кронштейн: картриджного типа | Шимано® | 49,1–68,7 | 435–608 |
| Shimano® Hollowtech® II | 34,5–49,1 | 305–435 | |
| Campagnolo® (трехсекционный) | 70 | 612 | |
| Чашки Campagnolo® Ultra-Torque® | 35 | 310 | |
| ФСА® | 39,2–49 | 347–434 | |
| Race Face® | 47,5 | 420 | |
| Труватив® | 33,9–40,7 | 300–360 | |
| Уайт Индастриз™ | 27 | 240 |
Зона переключателя и рычага переключения передач
| Компонент | Тип/марка | Ньютон-метры | Дюйм-фунты |
|---|---|---|---|
| Зажимной болт рычага двойного управления тормозом/переключателем | Шимано® СТИ™ | 6–8 | 53–70 |
| Кампаньоло® | 10 | 89 | |
| СРАМ® | 6–8 | 53–70 | |
| Рычаг переключения: вертикальный/плоский стержень | Шимано® СТИ™ | 5–7,4 | 44–69 |
| Рычаг переключения передач: поворотная рукоятка | Шимано® Ревошифт® | 6–8 | 53–70 |
| СРАМ® | 17 | 150 | |
| Рычаг переключения передач: MTB с большим пальцем | Шимано® СТИ™ | 2,4–3 | 22–26 |
| Хомут переднего переключателя | Кампаньоло® | 5 | 44 |
| Кампаньоло® | 7 | 62 | |
| Шимано® | 5–7 | 44–62 | |
| СРАМ® | 4,5 | 39,8 | |
| СРАМ® | 5–7 | 44–62 | |
| Стяжной болт троса переднего переключателя | Шимано® | 5-6,8 | 44–60 |
| Кампаньоло® | 5 | 44 | |
| Мавик® | 5–7 | 44–62 | |
| СРАМ® | 4,5 | 40 | |
| Болт крепления заднего переключателя | Шимано® | 8–10 | 70–86 |
| СРАМ® | 8–10 | 70–86 | |
| Кампаньоло® | 15 | 133 | |
| Стяжной болт троса заднего переключателя | Шимано® | 5–7 | 44–60 |
| СРАМ® | 4–5 | 35,4–44,2 | |
| Кампаньоло® | 6 | 53 | |
| Болт шкива заднего переключателя | Шимано® | 2,9–3,9 | 27–34 |
Область тормозного суппорта и рычага
| Компонент | Тип/марка | Ньютон-метры | Дюйм-фунты |
|---|---|---|---|
| Тормозные рычаги стойки | Шимано® | 6–8 | 53–69 |
| Авид® | 5–7 | 44–62 | |
| Кампаньоло® | 10 | 89 | |
| Крепление тормозного суппорта к раме: боковая тяга, двойная ось, центральная тяга | Шимано® | 7,8–9,8 | 70–86 |
| Кампаньоло® | 10 | 89 | |
| Кейн Крик® | 7,7–8,1 | 68–72 | |
| Тектро® | 8–10 | 69–89 | |
| Крепление тормозного суппорта к раме: линейное или консольное | Шимано® | 8–10 | 69–89 |
| СРАМ® | 5–6,8 | 45–60 | |
| Авид® | 4,9–6,9 | 43–61 | |
| Control Tech® | 11,3–13,6 | 100–120 | |
| Тектро® | 6–8 | 53–69 | |
| Тормозная колодка: Резьбовая шпилька | Авид® | 5,9–7,8 | 53–69 |
| Кампаньоло® | 8 | 71 | |
| Кейн Крик® | 6,3–6,7 | 56–60 | |
| Тектро® | 5–7 | 43–61 | |
| Шимано® | 5–7 | 43–61 | |
| СРАМ® | 5,7–7,9 | 50–70 | |
| Тормозная колодка: гладкая шпилька | Шимано® | 7,9–8,8 | 70–78 |
| Тормозная колодка: Боковые и двухшарнирные болты | Кампаньоло® | 8 | 72 |
| Кейн Крик® | 6,3–6,7 | 56–60 | |
| Шимано® | 6–8 | 53–69 | |
| Тектро® | 5–7 | 43–61 | |
| Стяжной болт тормозного троса: линейная тяга и консоль | Контрольная технология® | 4,5–6,8 | 40–60 |
| Шимано® | 6–7,8 | 53–69 | |
| СРАМ® | 5,6–7,9 | 50–70 | |
| Тектро® | 6–8 | 53–69 | |
| Стяжной болт тормозного троса: боковая тяга/двойная ось/центральная тяга | Кампаньоло® | 5 | 44 |
| Кейн Крик® | 7,7–8,1 | 68–72 | |
| Мавик® | 7–9 | 62–80 | |
| Шимано® | 6–8 | 53–69 | |
| Тектро® | 6–8 | 53–69 |
Дисковые тормозные системы
| Компонент | Тип/марка | Ньютон-метры | Дюйм-фунты |
|---|---|---|---|
| Диск ротора к ступице: стопорное кольцо | Авид® | 40 | 350 |
| Шимано® | 40 | 350 | |
| Дисковый ротор к ступице: болты M5 | Авид® | 6,2 | 55 |
| Хейс® | 5,6 | 50 | |
| Магура® | 3,8 | 34 | |
| Шимано® | 2–4 | 18–35 | |
| Крепление корпуса суппорта | Авид® | 9–10,2 | 80–90 |
| Хейс® | 12,4 9 с вилками Manitou | 110 80 с вилками Manitou | |
| Магура® | 5,7 | 51 | |
| Шимано® | 6–8 | 53–69 | |
| Тектро® | 6–8 | 53–69 | |
| Фитинги для гидравлических шлангов | Хейс® | 6,2 | 55 |
Формулы для преобразования других обозначений крутящего момента в ньютон-метры (Нм) и дюйм-фунты (дюйм-фунт):
- Нм = дюйм-фунт x 0,113
- Нм = фут-фунт x 1,356
- Нм = кг-см x 0,0981
- дюйм-фунт = фут-фунт x 12
- дюйм-фунт = Нм x 8,851
- дюйм-фунт = кгс-см x 0,87
Эквивалентность крутящего момента
| Newton Meter (NM) | Приблизительный дюйм-фунты (in-Lb. ) | . | 8,9 | 0,7 |
|---|---|---|---|---|
| 2 | 17,7 | 1,5 | ||
| 3 | 26,6 | 2,2 | ||
| 4 | 35,4 | 3,0 | ||
| 5 | 44,3 | 3,7 | ||
| 6 | 53,1 | 4,4 | ||
| 7 | 62,0 | 5,2 | ||
| 8 | 70,8 | 5,9 | ||
| 9 | 79,7 | 6,6 | ||
| 10 | 88,5 | 7,4 | ||
| 11 | 97,4 | 8.1 | ||
| 12 | 106,2 | 8,9 | ||
| 13 | 115,1 | 9,6 | ||
| 14 | 123,9 | 10,3 | ||
| 15 | 132,8 | 11.1 | ||
| 16 | 141,6 | 11,8 | ||
| 17 | 150,5 | 12,5 | ||
| 18 | 159,3 | 13,3 | ||
| 19 | 168,2 | 14,0 | ||
| 20 | 177,0 | 14,8 | ||
| 21 | 185,9 | 15,5 | ||
| 22 | 194,7 | 16,2 | ||
| 23 | 203,6 | 17,0 | ||
| 24 | 212,4 | 17,7 | ||
| 25 | 221,3 | 18,4 | ||
| 26 | 230,1 | 19,2 | ||
| 27 | 239,0 | 19,9 | ||
| 28 | 247,8 | 20,7 | ||
| 29 | 256,7 | 21,4 | ||
| 30 | 265,5 | 22,1 | ||
| 31 | 274,4 | 22,9 | ||
| 32 | 283,2 | 23,6 | ||
| 33 | 292,1 | 24,3 | ||
| 34 | 300,9 | 25,1 | ||
| 35 | 309,8 | 25,8 | ||
| 36 | 318,6 | 26,6 | ||
| 37 | 327,5 | 27,3 | ||
| 38 | 336,3 | 28,0 | ||
| 39 | 345,2 | 28,8 | ||
| 40 | 354,0 | 29,5 | ||
| 41 | 362,9 | 30,2 | ||
| 42 | 371,7 | 31,0 | ||
| 43 | 380,6 | 31,7 | ||
| 44 | 389,4 | 32,5 | ||
| 45 | 398,3 | 33,2 | ||
| 46 | 407. Разное |