Продажа квадроциклов, снегоходов и мототехники
second logo
Пн-Чт: 10:00-20:00
Пт-Сб: 10:00-19:00 Вс: выходной

+7 (812) 924 3 942

+7 (911) 924 3 942

  • 0

Двухступенчатый планетарный редуктор: Устройство и принцип действия двухступенчатого планетарного редуктора | Полезные статьи

Содержание

Устройство и принцип действия двухступенчатого планетарного редуктора | Полезные статьи

Понравилось видео? Подписывайтесь на наш канал! Продолжаем знакомить вас с устройством и принципом работы различных электрических устройств. Сегодня речь пойдет о планетарном редукторе. В данной статье мы рассмотрим такой вопрос, как устройство двухступенчатого планетарного редуктора, а также принцип его работы.

Планетарный редуктор устройство

 

• корпус редуктора, изготовленный из чугуна;

• венец второй ступени, выполненный из стали. Устанавливается внутрь корпуса редуктора;

• водило второй ступени;

• сателлиты; 

• подшипники, устанавливающиеся в сателлиты, которые монтируются в собранном виде в корпус водила второй ступени;

• оси сателлитов;

• верхние стопорные кольца, устанавливаемые на осях.

Сателлиты фиксируются осями в корпусе водила;

• далее на оси сателлитов устанавливаются нижние стопорные кольца;

• подшипник, который закрепляется изнутри задней части корпуса. В нем расположен вал водила второй ступени.

 

На вале водила второй ступени закрепляются следующие детали:

 

• дистанционная втулка;

• подшипник;

• стопорное кольцо;

• упорное кольцо;

• сальник;

• прокладка;

• крышка сквозная, фиксируемая болтами.

 

Также в редукторе присутствуют:

 

• отверстие для заливки масла, закрывающееся пробкой;

• подшипник центральной шестерни;

• центральная шестерня, устанавливаемая между сателлитами и хвостовиком внутрь центрального подшипника;

• опорный подшипник водила, расположенный на посадочном месте корпуса водила второй ступени;

• венец первой ступени, который находится в корпусе редуктора на опорном подшипнике водила второй ступени;

• корпус водила первой ступени;

• сателлиты;

• подшипники, устанавливаемые внутрь сателлитов. Сами сателлиты в сборе располагаются в корпусе водила первой ступени;

• оси сателлитов;

• установленные на осях верхние стопорные кольца и сателлиты, зафиксированные осями в корпусе водила;

• нижние стопорные кольца на оси сателлитов.

• подшипник опоры водила первой ступени, расположенный на посадочном месте корпуса водила. 

 

Собранное водило первой ступени монтируем на центральную шестерню опорным подшипником вовнутрь.

 

• второй опорный подшипник на посадочном месте;

• прокладка, закрепленная  на корпусе;

• передний щит, фиксируемый болтами к корпусу.

 

На вал электродвигателя надеваем передний сальник, втулку сальника и устанавливаем моторную шестерню. Соединяем редуктор с двигателем через отверстия во фланцах с помощью болтов.

 

Планетарный редуктор принцип работы 

Двухступенчатый планетарный редуктор работает следующим образом. Вращение вала электродвигателя с моторной шестерней приводит в движение сателлиты первой ступени. Они вращаются вокруг своей оси в направлении, противоположном вращению вала двигателя.

 

Поскольку коронная шестерня первой ступени зафиксирована неподвижно, сателлиты, помимо вращения вокруг своей оси, вынуждены вращаться внутри коронной шестерни в одном направлении с вращением вала двигателя, приводя в движение водило, на котором они закреплены.

 

Вращение водила первой ступени через центральную шестерню передается сателлитам второй ступени, которые начинают вращаться вокруг своей оси и внутри коронной шестерни второй ступени, приводя в движение водило второй ступени.

 

Мы рассказали об устройстве и принципе работы двухступенчатого планетарного редуктора. Вы также можете посмотреть наше видео, в котором мы детально показали двухступенчатый планетарный редуктор, его устройство и принцип работы.

Редуктор планетарный двухступенчатый. | PRO-TechInfo

Технические характеристики.

  1. Крутящий момент: 500 Н⋅м;
  2. Мощность: 2,66 кВт;
  3. Частота вращения тихоходного вала: 51 мин-1;
  4. Передаточное число: 27,9.

Основные данные зубчатых передач.

    1. Быстроходная ступень: u=6,64; z1=19; z2=44; z3=107; m=1,5;
    2. Тихоходная ступень: u=4,2; z4=20; z5=22; z6=64; m=2,5;
    3. Точность передач: 7-С ГОСТ 1643-81;
    4. Материал шестерен: сталь 40ХН, твердость 280…310 НВ;
    5. Материал зубчатых колес: сталь 45, твердость 167…194 НВ.

Описание устройства и работы планетарного редуктора.

Каждая ступень редуктора планетарного двухступенчатого состоит из двух центральных колес, из которых одно — с внешними зубьями ведущее (шестерня), второе с внутренними зубьями — неподвижное, и ведомого водила.

Для выравнивания нагрузки между сателлитами центральная шестерня каждой ступени соединена с ведущим валом (водилом) зубчатой муфтой, выполняющей роль шарнира. Центральная шестерня не имеет опор и может перемещаться в радиальных направлениях, если силы в зацеплениях с сателлитами неодинаковые (плавающая шестерня). От осевых перемещений шестерня зафиксирована проволочными кольцами, расположенными в проточках зубчатых полумуфт. Глубина проточек такова, что при сближении отогнутых концов кольцо уменьшается в диаметре и не задевается за вершины зубьев полумуфты при сборке (см. разрез Е — Е).

В тихоходной ступени четыре сателлита. Для выравнивания нагрузки между ними центральная шестерня выполнена плавающей, а оси сателлитов — податливыми (полыми).

Центральное неподвижное колесо первой ступени выполнено с диафрагмой, в ступице которой установлены шарикоподшипники водила.

Подшипники смазываются маслом, разбрызгиваемым сателлитами.

Соседние страницы

Редукторы планетарные двухступенчатые

Редукторы планетарные двухступенчатые

Для получения передаточных чисел от 10 до 60 могут быть использованы двухступенчатые редукторы со ступенями, выполненными по схеме 2K-h.

Двухступенчатые редукторы, выполненные по схеме 2K-h, с двухвенцовыми сателлитами, в обоих ступенях могут иметь передаточные числа от 60 до 400.

Двухступенчатые планетарные редукторы этой же схемы используются для получения крутящих моментов до 4000 кН • м.

В силовых установках, в двухступенчатых редукторах можно получить передаточные числа до 60 и более, Передаточные числа свыше 50 уменьшают число зубьев на центральных шестернях и уменьшают срок службы редуктора. При этом повышается уровень шума. Поэтому сумма передаточных чисел не должна превышать 50,

Редуктор планетарный двухступенчатый блочный

На листе 111 приведена конструкция редуктора, выполненная по схеме 2K-h. В торцевой крышке на двух подшипниках установлен вал, откованный вместе с центральной шестерней первой ступени передач. Опорами сателлитов служат двухрядные сферические и роликовые подшипники. Водило первой ступени соединяется с центральной шестерней второй ступени через зубчатое соединение.

 

 

Сателлиты второй ступени установлены на двух двухрядных роликовых подшипниках, водило установлено на двух однорядных цилиндрических роликоподшипниках. Водила первой и второй ступени имеют жесткую конструкцию. Внутренние зубья центрального колеса первой ступени нарезаны на внутреннем выступе корпусной детали. Кованое центральное колесо второй ступени из легированной стали с общей термической обработкой. Колесо болтовым соединением объединено с корпусными деталями. Смазываются зацепление и подшипники маслом, залитым в картер редуктора. Валы уплотняются манжетными уплотнениями. Характерной особенностью редуктора является его блочность и удобство сборки. Отдельно собирается торцевая крышках валом и подшипниками и водило с сателлитами первой и второй ступени.

 

 Редуктор планетарный двухступенчатый с плавающими венцами

В двухступенчатом планетарном редукторе (лист 112) с передаточным числом и = 51,3 консольное центральное колесо быстроходной ступени редуктора опирается с одной стороны на два однорядных шариковых подшипника, размещенных в левой щеке водила. Каждый сателлит первой ступени установлен на однорядном шариковом подшипнике, который опирается на ось, установленную неподвижно в щеках водила.

Правая щека с помощью цилиндрических штифтов соединена со шлицевой втулкой. Движение на центральное колесо второй ступени передается через шлицевое соединение втулки с валом. Опорами каждого сателлита второй ступени служат два однорядных шариковых подшипника. Водила обеих ступеней неразъемные, что значительно упрощает их конструкцию. Водило второй ступени выполнено как одно целое с тихоходным валом и опирается на два однорядных шариковых подшипника. Центральные колеса с внутренними зубьями первой и второй ступени выполнены плавающими и застопорены от вращения зубчатыми муфтами.

Наружные зацепления зубчатых муфт с одной стороны входят в зацепление с зубьями центрального колеса, а с другой — соединяются с венцами, закрепленными неподвижно в корпусе редуктора. Муфты и центральные колеса о внутренним зацеплением удерживаются от осевого смещения пружинными кольцами, установленными в канавках центрального колеса и неподвижного венца. Использование плавающих центральных колес дает возможность выравнивать нагрузку между сателлитами по длине зубьев и тем самым повышать передаваемый момент.

Введение плавающих центральных колес и зубчатых муфт ведет к усложнению конструкции редуктора, поэтому их используют только при высоких частотах вращения.

Редуктор планетарный двухступенчатый с двухвенцовыми сателлитами

Двухступенчатые редукторы с двухвенцовыми сателлитами в силовых установках могут иметь передаточное число до 400, а в кинематических — до 600, выполненных по схеме 2K-h обеих ступеней. При использовании эффективных методов поверхностного упрочнения зубьев можно достичь и наименьшего расхода металла на единицу передаваемого момента, по сравнению с другими видами передач.

На листе 113 показан двухступенчатый планетарный редуктор с передаточным числом и =167. Конструктивное исполнение как первой, так и второй ступени аналогично ранее рассмотренной конструкции одноступенчатого редуктора с двухвенцовыми сателлитами.

Вторая ступень редуктора передает больший момент, чем первая ступень, и поэтому водило установлено на однорядных роликовых конических-подшипниках. Корпус редуктора сварной. Для устранения возможной деформации корпус подвергается термической обработке для снятия внутренних напряжений, вызываемых нагревом при сварке. Масло заливается в картер корпуса, и зацепление смазывается купанием в ванне, а подшипники — разбрызгиванием.

Редуктор планетарный двухступенчатый с плавающими венцами второй ступени

В двухступенчатых планетарных редукторах, при исполнении первой ступени по схеме 2K-h, а второй — по схеме 3К, можно получить передаточные числа от 60 до 600 при высоком КПД и при небольшой массе на единицу передаваемого момента.

На листе 114 представлен двухступенчатый планетарный редуктор с передаточным числом и = 286. Со стороны быстроходного вала планетарная передача выполнена по схеме 2K-h. Быстроходный вал откован как одно целое с центральной шестерней и опирается на два однорядных шариковых подшипника. Сателлиты, входящие в зацепление с центральной шестерней и с центральным колесом с внутренним зацеплением, в качестве опор имеют по два цилиндрических подшипника с короткими цилиндрическими роликами, с двумя буртами наружного кольца одним буртом на внутреннем кольце. Между наружными кольцами установлено пружинное кольцо в канавке отверстия сателлита и распорное кольцо, что устраняет осевое перемещение колец. Внутренние кольца подшипников от осевого смещения предохраняются двумя кольцами, установленными между торцевыми поверхностями подшипников и щеками водила. С водила движение через шлицевое соединение передается на вал центральной шестерни второй ступени, выполненной по схеме 3К.

Сдвоенные сателлиты опираются на сферические двухрядные роликоподшипники, внутренние кольца которых посажены на неподвижные оси, закрепленные с одной стороны планками и болтами к щекам родила. Для обеспечения самоустановки сателлитов и равномерного распределения нагрузки по длине зубьев центральные колеса с внутренними зацеплениями, неподвижное и подвижное, имеют соединения через зубчатые муфты. На валах установлены двойные севанитовые уплотнения.

Смазывание зацеплений происходит окунанием в масло, налитое в картер, а подшипников — разбрызгиванием. Для отвода теплого воздуха и паров масла на верхней части корпуса установлен вентиляционный колпак.

Габаритные и присоединительные размеры редукторов (лист 115) даны в табл. 187.

 

 

Таблица 187

Габаритные и присоединительные размеры планетарных двухступенчатых редукторов с плавающими венцами второй ступени (лист 115), мм

 

 

 

 

Редуктор планетарный двухступенчатый усиленной конструкции

Редукторы этого типа используются в цементной промышленности для привода крупных высокопроизводительных цементных трубных мельниц.

Редукторы изготовляются с передаточными числами от 30 до 60, с передаваемыми моментами до 3000 кН • м, работают в непрерывном длительном режиме.

На листе 116 представлен двухступенчатый редуктор с радиусами водил первой и второй ступени r1= 462 мм и r2= 700 мм.

Центральная шестерня первой ступени плавающая, соединяется с валом электродвигателя через зубчатую муфту. Сателлиты первой ступени установлены на двухрядных роликовых сферических подшипниках, насаженных на пустотелые валики, последние закрепляются болтами к щекам водила. Опорами водила с одной стороны служит цилиндрический двухрядный роликовый подшипник, а с другой — сферический двухрядный роликовый подшипник.

Сферический подшипник неподвижно закреплен в корпусе по наружному и внутреннему кольцам и устраняет осевое перемещение водила. Водило первой ступени соединяется с центральной шестерней второй ступени зубчатой муфтой. Раздвоенные сателлиты опираются на два сферических роликовых подшипника. Таким образом обеспечивается самоустановка каждой части сателлита по зубьям центральной шестерни и колеса.

Опорами для водила служат цилиндрический роликовый подшипник и двухрядный сферический роликоподшипник, последний жестко установлен в корпусе.

В отверстие водила с допусками горячей посадки запрессован тихоходный вал. Центральные колеса первой и второй ступени болтовыми соединениями жестко связаны с корпусными деталями. Сварные корпус и крышка — из листового металла.

Особое внимание уделено обильному смазыванию всех трущихся деталей редуктора. К центральным шестерням смазка подводится через брызгалы. Двухрядные сферические подшипники имеют подвод смазки с двух сторон зацеплению зубчатых муфт непрерывным потоком подается масло специальными соплами. Такое обильное снабжение охлажденным и отфильтрованным маслом зацепления и подшипников гарантирует надежность непрерывно работающего редуктора.

Смотрите также

Мотор-редуктор планетарный двухступенчатый 3МП-63 (4МП-63)​

Мотор-редуктор планетарный двухступенчатый 3МП-63 (4МП-63)​

Наше предприятие предлагает вам купить редуктор планетарный высокого качества по низкой цене. Также у нас вы можете купить мотор-редуктор. Все промышленное оборудование, которое поставляется ООО «АТЛАНТ-ТМ» соответствует высоким стандартам качества, и зарекомендовало себя как надежное и долговечное.

Редуктор планетарного типа для изменения скоростей вращения и момента вращения использует планетарную передачу. Даная передача включает в себя солнечную шестерню, которая расположена в центре редуктора, на краю редуктора расположен зубчатую корону, также ее называют – эпицикл, между ними находятся шестерни меньшего диаметра – сателлиты. Благодаря зацеплению данной системы шестерней между собой изменяется крутящий момент и частота вращения.

Производители со всего мира создают множество разновидностей редукторов и моторов-редукторов планетарного типа. Они используются при установках на общепромышленных агрегатах в любых видах хозяйства. Среди наиболее распространенных можно отметить редуктор 3МП, мотор-редуктор 3МП, редуктор 4МП.

Планетарная передача в данных редукторах и моторах-редукторах может быть одноступенчатой, двухступенчатой и трехступенчатой. Чем больше количество ступеней, тем большего передаточного числа можно достичь в процессе его эксплуатации.

Двухступенчатый мотор-редуктор соединяет в себе планетарный редуктор с двумя ступенями передач и асинхронный электрический мотор.

Благодаря своей уникальной конструкции планетарные редукторы обладают высокими показателями эффективности. Но из за своей сложности данные редуктора мене распространены нежели цилиндрические или червячные. Если сравнивать с цилиндрическими — они более компактны. Если сравнивать с червячными – обладают высшим  коэффициентом полезного действия и большей долговечностью. 

Габаритные и присоединительные размеры, мм

Типоразмер планетарного редуктора, мотор-редуктора

Размеры, мм

А

А1

В

B1

H

h2

L

L1max

L2

L3

d

c

ЗМП-63

2802303252604201605101000140332430

Технические характеристики

Частота вращения выходного вала, об/минКрутящий момент, Н.мЭл/дв.P, кВт
двухступенчатые
181131АИР112МА82,2
1542АИР112МВ83
22,41239АИР112МА63
1652АИР112МВ64
28991АИР112МА63
1322АИР112МВ64
35,51320АИР112М45,5
1000АИР100L44
451120АИР112М45,5
1500АИР132S47,5
56950АИР112М45,5
1225АИР132S47,5
711000АИР132S47,5
1400АИР132М411
901130АИР132М211
1120АИР160М811

Планетарный редуктор — это.

.. Что такое Планетарный редуктор?

Планетарный редуктор (дифференциальный редуктор) — один из классов механических редукторов. Редуктор называется планетарным из-за планетарной передачи, находящейся в редукторе, передающей и преобразующей крутящий момент. Планетарный редуктор может быть с одной или более планетарными передачами.

Устройство и принцип действия планетарного редуктора

Устройство планетарного редуктора
  • Солнечная шестерня — в центре редуктора.
  • Коронная шестерня — на периферии редуктора.
  • Сателлиты — три малые шестерни между солнечной и коронной.
  • Водило — не показано, механически соединяет все сателлиты, на осях водила сателлиты вращаются.

Вращение от главной передачи передаётся через полуоси на солнечную шестерню. Солнечная шестерня вращает сателлиты, они вращаются на своих осях, а оси закреплены на водиле, водило — на балке моста. Сателлиты, вращаясь, передают вращение коронной шестерне, а они — к ступице. Крутящий момент увеличивается во столько раз, во сколько раз количество зубьев на солнечной шестерне меньше количества зубьев на коронной.

Применение планетарных редукторов

Планетарный редуктор в ведущих мостах

В ведущих мостах грузовых автомобилей МАЗ, автобусов Ikarus, троллейбусов ЗиУ-9, тракторов Т-150К, К-700 применяются планетарные редукторы, передающие крутящий момент от полуоси к ступице колеса. Применение планетарного редуктора в бортовой передаче (разнесённая передача) позволяет уменьшить диаметр главной передачи и, следовательно, увеличить дорожный просвет, а также уменьшить диаметр полуосей, спроектировав их на меньший крутящий момент.

В ведущем автомобильном мосту можно обойтись и без планетарных передач при том же передаваемом крутящем моменте, например мост автомобилей КАМАЗ имеет сходные характеристики с ведущим мостом автомобилей МАЗ, только на КАМАЗе главная передача двойная, а на МАЗе — одинарная.

Планетарные редукторы в автоматической коробке передач

Автоматическая коробка передач в разрезе

В автоматических коробрах перемены передач крутящий момент передаётся от вала с солнечной шестернёй на вал связанный с водилом.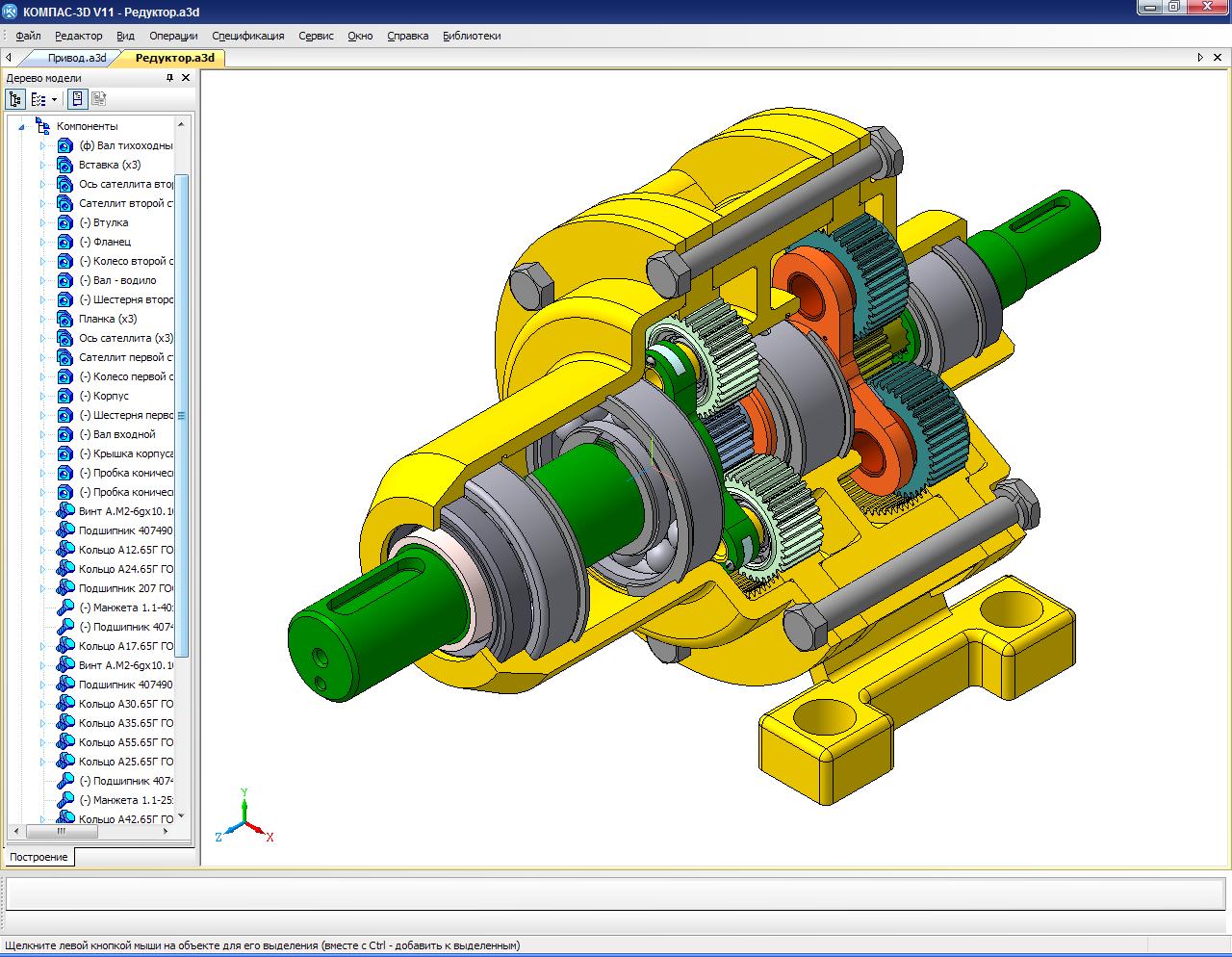 Если коронная шестерня будет заторможена — тогда сателлиты будут обкатываться вокруг солнечной и коронной шестерён, приводя во вращение водило. Передаточное число редуктора будет равняться отношению числа зубьев на солнечной шестерне к числу зубьев на коронной. Если коронную шестерню отпустить (растормозить) — тогда крутящий момент будет передаваться напрямую, отношение 1:1. В современных конструкциях автоматических коробок перемены передач чаще всего встречается планетарный механизм Лапелетьера. [1]

Промышленность России выпускает планетарные редукторы серий 3П и 3МП. Планетарные редукторы имеют большую популярность среди механических редукторов. Она достигается благодаря малым габаритам планетарных редукторов, высокому КПД, большому передаточному числу.

Шарикоподшипник

Шарикоподшипник представляет пример планетарного редуктора, в котором водилом является сепаратор, функции солнечной шестерни выполняет внутреннее кольцо, функции коронной шестерни — наружное кольцо, а сателлиты — это шарики.

На приведённой анимации обратите внимание, что скорость вращения внутреннего кольца заметно больше, чем скорость вращения сепаратора с шариками. Если отпустить наружное кольцо — то скорости вращения сравняются (будет включена «прямая» передача). Если затормозить водило — то будет вращаться наружное кольцо (ступица в заднем мосту троллейбуса или автомобиля МАЗ).

С использованием обыкновенных шарикоподшипников могут быть сконструированы маломощные планетарные редукторы (для научных или измерительных приборов). Например, шарикоподшипники используются в конструкции верньера, применяемого для точной настройки радиостанции на нужную радиоволну.

См. также

Примечания

Ссылки

Видео редуктора

Мотор-редуктор планетарный двухступенчатый МПО-2М — Гормаш

Назначение: Мотор-редукторы серии МПО-2М предназначены для комплектации малогабаритного оборудования, также могут быть использованы в качестве привода общегоназначения. Мотор-редуктор представляет собой блок асинхронного обдуваемого электродвигателя и планетарного редуктора.

Габаритные и присоединительные размеры мотор-редуктора МПО-2М -15-В-2469-0,55/0,56-У3

 

Диапазон крутящих моментов на выходном валу, Нxм

Диапазон передаточных отношений

Диапазон мощностей электродвигателей, кВт

Исполнение по монтажу

133 3350

22,8 2469

0,37 15

В; ВК; Ф; Щ

 

Технические характеристики мотор-редуктора МПО-2М -15-В-2469-0,55/0,56-У3

Допускаемый крутящий момент на выходном валу, Нxм

2064

Частота вращения выходного вала, об/мин

0,56

Передаточное отношение

2469

Исполнение по монтажу

В

Электродвигатель

Типоразмер

АИР71А4

Мощность, кВт

0,55

Частота вращения, об/мин

1500

Масса, кг

9,8

Масса мотор-редуктора, кг

186

 

Условия эксплуатации:
— режим работы S1 по ГОСТ 183 продолжительность работы по 8 — 24 ч/сут;
— нагрузка постоянная или переменная в пределах номинального крутящего момента;
— атмосфера типа I и II по ГОСТ 15150 при запыленности воздуха не более 10 мг/м3;
— окружающая среда — неагрессивная, невзрывоопасная, относительной влажностью до 80%;
— климатические исполнения — У2, У3, Т2 и Т3 по ГОСТ 15150. _

Условное обозначение:
МПО-2М — тип мотор-редуктора
n — номинальная частота вращения выходного вала (об/мин)
D — условный диаметр водила
N — мощность электродвигателя (кВт)

В — вертикальное с опорным фланцем , выходным валом вниз;
ВК — вертикальное с опорным фланцем, выходным валом вниз и кольцевой канавкой на нём;
Щ — горизонтальное на опорных лапах;
Ф — горизонтальное с опорным фланцем

Пример обозначения мотор-редуктора МПО-2М -15-В-2469-0,55/0,56-У3:
мотор-редуктор типа МПО-2М с условным диаметром водила 15, исполнением по монтажу — вертикальным (В) с опорным фланцем, передаточным отношением 2469, мощностью электродвигателя 0,55 кВт, номинальная частота вращения выходного вала 0,56 об/мин, климатическим исполнением У и категорией размещения 3 по ГОСТ 15150.

Заказывайте Мотор-редуктор планетарный двухступенчатый 3МП40 (18-90) об. от «ООО «ГИДРОМЕХАНИКА»»

Мотор-редуктор планетарный двухступенчатый 3МП40 (18-90) об. 

ООО фирма «ПОЛИМЕТ» является поставщиком качественных редукторных механизмов.

Редуктор — это механическое устройство, которое передает и преобразует крутящий момент, имея при этом ординарное или же множественное количество механических передач. Редукторы применяются в различных отраслях хозяйства и используются в различных агрегатах. Главными характеристиками редукторных механизмов выступают: коэффициент полезного действия, количество валов, их угловые скорости, тип ступеней и передач, передаточное отношения и мощность, а также крутящий момент и скорость вращения основного вала. Основной задачей редуктора выступает превращение скорости вращения, в зависимости от наших нужд, в большую или меньшую, изменяя при этом вращающий момент. Так редуктор, превращающий большую скорость вращения в меньшую, называется — демультипликатор. Мультипликатор, в свою очередь, превращает меньшую скорость вращения в большую, понижая при этом вращающийся момент.

В зависимости от принципа действия редукторные механизмы делятся на несколько типов. Основным классификатором выступает тип механических передач. В соответствии с ним редукторные механизмы бывают:

1. Цилиндрические редукторы ЦУ, 1ЦУ, 1Ц2У, 1Ц2Н, 1МЦ2С, РМ состоят из корпуса, в котором помещены рабочие колеса, валы с подшипниками и система их смазки. За принципом действия они демультипликаторы.

Данные типы редукторов есть одними из наиболее популярных в связи со своей простотой устройства и высокими характеристиками. Они применяются в приводах грузовых кранов, в электроприводах техники или стают компонентом моторов-редукторов. Цилиндрические редукторы работают без особых проблем в любых условиях (как беспрерывно, так и с периодическими остановками, при постоянных и переменных нагрузках).

2. Червячные редукторы Ч , 1Ч, 2Ч имеют внутри червячную механическую передачу, в основе которой лежит винт, внешне похож на червяка отсюда и название. Они также являются демультипликаторами и преобразовывают большую скорость вращения в меньшую, увеличивая вращающийся момент. Они могут применяться практически везде, где нужно недорогое решение по снижению частоты вращения и увеличению крутящего момента при отсутствии значительных ударных нагрузок и недлительной работы.

3. Планетарные редукторы 3МП, 4МП названы так в связи с планетарной передачей, имеющейся внутри. Планетарные редукторы используются в различных агрегатах, среди которых, например, грузовые лебедки, электроинструмент, мосты и колеса и прочие. Из за более сложной конструкции данный редуктор менее распространен чем два предыдущие виды.

На все редукторы имеется гарантия, как доказательство их надежности и долговечности.

Габаритные и присоединительные размеры, мм

 

Типоразмер планетарного редуктора, мотор-редуктораРазмеры, мм
АА1ВB1HH1LL1maxL2L3dc
ЗМП-40210170220180280112390760110351920

 

Технические характеристики
Частота вращения выходного вала, об/минКрутящий момент, Н. мЭл/дв.P, кВт
двухступенчатые
                                                 Мотор-редуктор 3МП40 (18-90) об.  
18375АИР90LA80,75
283АИР80В80,55
22,4375АИР80В61,1
227АИР71В60,55
28364АИР80В61,1
248АИР80А60,75
35,5375АИР80В41,5
287АИР80А41,1
45308АИР80В41,5
226АИР80А41,1
56364АИР90L42,2
248АИР80В41,5
71375АИР90L23
287АИР80В22,2
90308АИР90L23
226АИР80В22,2

Многоступенчатая коробка передач — Neugart USA Corp.

В одинарных прямозубых шестернях пара шестерен образует ступень шестерни. Если вы соедините несколько зубчатых пар друг за другом, это называется многоступенчатой ​​коробкой передач. На каждой ступени редуктора направление вращения между ведущим валом и выходным валом меняется на противоположное. Общий коэффициент умножения многоступенчатых редукторов рассчитывается путем умножения передаточного числа каждой ступени редуктора.

Скорость движения уменьшается или увеличивается на коэффициент передаточного числа, в зависимости от того, является ли это передаточным числом: «медленное» или «быстрое».В большинстве случаев требуется отношение к медленному, поскольку крутящий момент привода умножается на общий коэффициент умножения, в отличие от скорости привода.

Многоступенчатая прямозубая шестерня может быть реализована технически значимым образом до передаточного числа приблизительно 10: 1. Причина этого кроется в соотношении количества зубов. При передаточном числе 10: 1 ведущая шестерня очень мала. Это отрицательно сказывается на геометрии зуба и передаваемом крутящем моменте.С планетарной передачей очень легко реализовать многоступенчатую коробку передач.

Двухступенчатая или трехступенчатая коробка передач может быть получена простым увеличением длины зубчатого венца и последовательным размещением нескольких отдельных планетарных ступеней. Планетарная передача с передаточным числом 20: 1 может быть изготовлена, например, с индивидуальными передаточными числами 5: 1 и 4: 1. Вместо ведущего вала водило планетарной передачи содержит солнечную шестерню, которая приводит в движение следующую ступень планетарной передачи. Трехступенчатая коробка передач получается за счет увеличения длины зубчатого венца и добавления еще одной планетарной ступени.Передаточное число 100: 1 достигается с использованием индивидуальных передаточных чисел 5: 1, 5: 1 и 4: 1. В принципе, все индивидуальные передаточные числа можно комбинировать, что приводит к большому количеству вариантов передаточных чисел для многоступенчатых планетарных редукторов. При этом передаваемый крутящий момент можно увеличить с помощью дополнительных планетарных шестерен. Направление вращения приводного вала и выходного вала всегда одинаково, при условии, что коронная шестерня или корпус зафиксированы.

По мере увеличения числа ступеней редуктора эффективность всей коробки передач снижается.При соотношении 100: 1 КПД ниже, чем при соотношении 20: 1. Чтобы противодействовать этой ситуации, при использовании многоступенчатых редукторов необходимо учитывать тот факт, что потери мощности приводной ступени невелики. Это достигается, например, за счет уменьшения потерь на трение в уплотнении редуктора или за счет меньшего геометрического размера ступени привода. Это также снижает инерцию массы, что является преимуществом в динамических приложениях. Одноступенчатые планетарные редукторы являются наиболее эффективными.

Многоступенчатые редукторы также могут быть реализованы путем комбинирования различных типов зубьев.В прямоугольном редукторе просто сочетаются коническая передача и планетарный редуктор.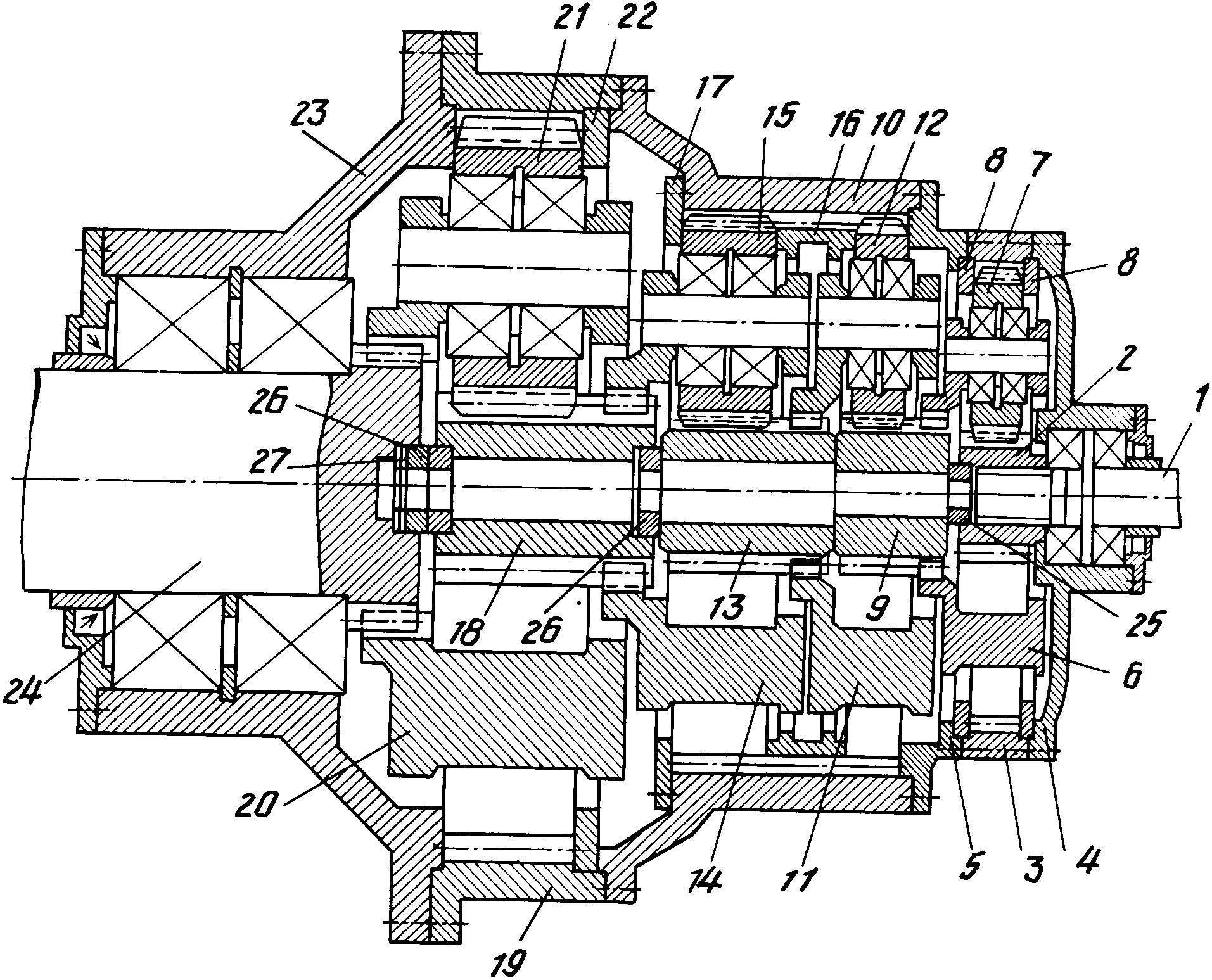 Здесь также общий коэффициент умножения является произведением индивидуальных соотношений. В зависимости от типа зубчатой ​​передачи и типа конической зубчатой ​​передачи привод и выход могут вращаться в одном направлении.

Преимущества многоступенчатых редукторов:
  • Широкий диапазон передаточных чисел
  • Постоянное вращение планетарных шестерен
  • Компактная конструкция с высокими передаточными числами
  • Возможна комбинация различных типов редукторов
  • Широкий спектр применения
Недостатки многоступенчатых редукторов (по сравнению с одноступенчатыми):
  • Более сложная конструкция
  • Низкий КПД

Что такое многоступенчатые редукторы и когда они используются?

Редукторы обычно используются в приложениях управления движением для изменения выходной скорости и крутящего момента от двигателя к ведомому компоненту.При использовании меньшей шестерни с меньшим количеством зубьев (обычно называемой шестерней) для привода более крупной шестерни с большим количеством зубьев крутящий момент, передаваемый нагрузке, увеличивается, а скорость вращения нагрузки уменьшается.

В коробках передач с цилиндрическими, косозубыми или коническими зубчатыми колесами передаточное число — величина увеличения крутящего момента и уменьшения скорости — представляет собой просто отношение количества зубьев ведомой (большей) шестерни к количеству зубьев ведущей ( меньшую, или ведущую) шестерню.

Теоретически можно получить любое передаточное число, регулируя количество зубьев на ведущей и ведомой шестернях, но в реальных условиях высокие передаточные числа создают проблемы проектирования, такие как необходимость в очень маленькой шестерне (ведущей шестерне). , высокие нагрузки на зубья шестерни и ограниченные возможности передачи крутящего момента. К счастью для конструкторов машин, эти проблемы можно легко решить с помощью многоступенчатой ​​коробки передач.

Расчет передаточного числа для одноступенчатой ​​планетарной коробки передач зависит от того, какие шестерни являются ведомой, неподвижной и выходной.В большинстве планетарных редукторов, используемых для управления движением, солнце является ведомой шестерней, коронная шестерня неподвижна, а водило приводит в движение выходной вал. Для этой конфигурации передаточное число (i p ) равно единице плюс отношение зубьев коронной шестерни (Z r ) к зубцам солнечной шестерни (Z s ), или i p = 1 + Z r / Z с .

Многоступенчатая коробка передач просто объединяет две или более пары или ступени шестерен, при этом выход одной ступени соединяется с входом следующей.Полученное передаточное число является произведением передаточных чисел каждой ступени. Например, двухступенчатая коробка передач, состоящая из одной ступени с передаточным числом 5: 1 и второй ступени с передаточным числом 3: 1, обеспечивает выходное передаточное число 15: 1 (5 x 3), поэтому крутящий момент, передаваемый на нагрузка в 15 раз превышает крутящий момент, создаваемый двигателем, без учета потерь при передаче, а скорость, передаваемая нагрузке, составляет 1/15 скорости двигателя.

В отличие от многоступенчатых коробок передач, которые состоят из параллельных шестерен, многоступенчатый планетарный редуктор, как показано в этом видео от Neugart, состоит из ступеней, которые соединены концентрически, что дает им более компактную площадь, чем параллельные конструкции при очень высоком понижении нужны соотношения.

Многоступенчатые редукторы могут состоять и часто состоят из различных типов зубчатых передач на каждой ступени. Например, прямоугольный планетарный редуктор может быть сконструирован с планетарной ступенью и спирально-конической ступенью. И, как показано в приведенном выше примере, величина редукции для каждой ступени может быть разной, но многоступенчатые редукторы обычно проектируются с более высоким передаточным числом на входе и более низким передаточным числом на выходной стороне.

Общий КПД многоступенчатой ​​коробки передач (или подходящую оценку) можно найти, умножив КПД каждой ступени.И важно отметить, что каждая ступень меняет направление вращения между входом и выходом, за исключением планетарной ступени, в которой направление вращения сохраняется между входом и выходом.

Для большинства одноступенчатых редукторов направления вращения входного и выходного валов противоположны, в то время как для двухступенчатых редукторов дополнительное изменение направления второй ступенью приводит к тому, что выходной вал вращается так же, как и входной вал, поскольку показано на рисунке ниже.

В большинстве одноступенчатых редукторов выходной вал вращается в направлении, противоположном входному. Но с каждой дополнительной ступенью направление вращения снова меняется на противоположное. Таким образом, в показанном здесь двухступенчатом редукторе выход вращается в том же направлении, что и вход.
Изображение предоставлено: KSB

Хотя КПД в некоторой степени снижается, многоступенчатые редукторы предлагают более высокие передаточные числа, чем можно было бы достичь с помощью большинства конструкций одноступенчатых редукторов. И они делают это в компактном корпусе, который можно оптимизировать для достижения наилучшего сочетания способности передачи крутящего момента, низкой инерции и высокой эффективности.

Червячные передачи обеспечивают очень высокие передаточные числа в одноступенчатой ​​передаче — в некоторых случаях до 60: 1 или больше — без сложности, связанной с несколькими зубчатыми передачами, хотя их эффективность обычно ниже, чем у многоступенчатых конструкций.

Анализ динамического поведения многоступенчатой ​​планетарной зубчатой ​​передачи, используемой в ветряном генераторе

Предлагается создать динамическую модель многоступенчатой ​​планетарной зубчатой ​​передачи, состоящей из двухступенчатой ​​планетарной зубчатой ​​передачи и одноступенчатой ​​планетарной зубчатой ​​передачи с параллельной осью. Используется в ветряных генераторах для анализа влияния скорости вращения и погрешности сетки на характеристики распределения динамической нагрузки на основе теории сосредоточенных параметров.Динамическое уравнение модели решается численным методом для анализа равномерного распределения нагрузки системы. Показано, что на свойство распределения нагрузки системы существенно влияют погрешность сетки и скорость вращения; Коэффициент распределения нагрузки и скорость изменения внутреннего и внешнего зацепления системы очевидны друг от друга.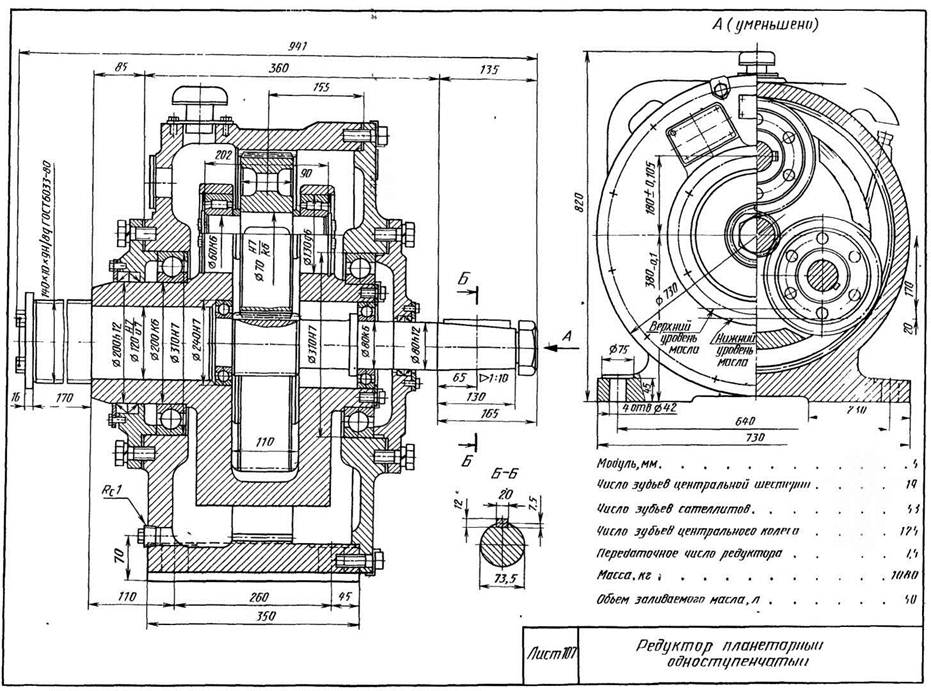 Исследование представляет собой полезное теоретическое руководство для проектирования многоступенчатой ​​планетарной зубчатой ​​передачи ветрогенератора.

1. Введение

Планетарный редуктор, обладающий преимуществами большого передаточного числа, простой конструкции, компактности и плавности хода, широко применяется во многих машинах. Несмотря на эти преимущества, планетарные шестерни могут иметь нежелательные динамические характеристики, приводящие к сильному шуму, вибрации и другим неприемлемым характеристикам. Был опубликован ряд статей по динамике планетарной передачи, которые включают модели с сосредоточенными параметрами и деформируемые или гибридные модели различной сложности [1–7].Модальный анализ был выполнен Lin и Parker [8] и Bodas et al. [9–13], которые подчеркнули структурные модальные свойства одноступенчатых двигателей и показали, что могут существовать только режимы планет, вращения и поступательного движения. Важно понимать основную причину неравномерного распределения нагрузки в планетарных трансмиссиях. Приложенный входной крутящий момент теоретически должен распределяться между каждой планетой -планетой; то есть каждый путь солнечной шестерни и кольца должен нести общий крутящий момент. Однако в реальных передачах существует неравное распределение нагрузки между параллельными трактами.Du et al. В [14] были найдены уравнения совместимости деформаций и уравнения баланса крутящего момента для системы планетарной трансмиссии 2-го типа на основе того признака, что система состоит из замкнутого контура потока мощности. С учетом погрешности изготовления, погрешности сборки и смещения деталей коэффициент распределения нагрузки каждой планетарной передачи был рассчитан с использованием теории эквивалентной погрешности зацепления и эквивалентной жесткости зацепления. Гу и Велекс [15] представили оригинальную модель планетарных шестерен с сосредоточенными параметрами для учета ошибок положения планет и моделирования их вклада в распределение динамической нагрузки между планетами.Сингх [16] разработал концепцию карты распределения эпициклической нагрузки для описания характеристик распределения нагрузки каждой планетарной зубчатой ​​передачи при любой ошибке положения и уровне крутящего момента. Комплексное экспериментальное исследование [17] было проведено для изучения поведения распределения нагрузки в семействе эпициклических зубчатых передач с различным числом планет. Эксперименты проводились при нескольких уровнях погрешности и крутящего момента. Результаты ясно показали влияние позиционных ошибок и то, что чувствительность эпициклического зубчатого колеса увеличивалась с увеличением количества планет.Дано физическое объяснение [18] поведения распределения нагрузки. Нагрузка, необходимая для создания необходимой деформации, является причиной неравномерного распределения нагрузки. Это объясняет эффективность системного плавающего режима в сокращении неравенства распределения нагрузки. Лу и др. [19] представили расчетную модель одноступенчатой ​​планетарной передачи с динамическим способом изучения поведения распределения нагрузки каждой планетарной передачи и проанализировали взаимосвязь между ошибкой и распределением нагрузки. Ye et al. [20] построили аналитическую модель планетарной зубчатой ​​передачи NGW с неравными модулями упругости и углами давления и проанализировали поведение распределения нагрузки каждой планетарной передачи.

Хотя имеющиеся ссылки ориентированы на разные области, большинство из них основано на математической модели одноступенчатой ​​планетарной зубчатой ​​передачи. О динамической модели многоступенчатой ​​планетарной передачи сообщается мало. Приведены некоторые сообщения о динамической модели многоступенчатой ​​планетарной зубчатой ​​передачи, состоящей из двухступенчатой ​​планетарной передачи и одноступенчатой ​​параллельной оси, и ее динамических характеристиках распределения нагрузки.

В данной работе предлагается схема трансмиссии двухступенчатого планетарного редуктора с разделением нагрузки, используемого в ветрогенераторе.Получено передаточное число планетарной зубчатой ​​передачи, а также взаимосвязь между передаточным отношением и характеристическим параметром планетарной зубчатой ​​передачи в соответствии с методом механизма преобразования и общей взаимосвязью между скоростью каждого блока в планетарной зубчатой ​​передаче. Динамическая модель многоступенчатой ​​зубчатой ​​передачи с разделением нагрузки, состоящей из двухступенчатой ​​планетарной зубчатой ​​передачи и одноступенчатой ​​зубчатой ​​передачи с параллельными осями, построена на основе теории сосредоточенных параметров и влияния скорости вращения и погрешности зацепления на характеристику распределения динамической нагрузки. системы.

2. Двухступенчатая планетарная зубчатая передача с разделением нагрузки
2.1. Кинематическая схема

Кинематическая схема двухступенчатой ​​планетарной передачи с разделением нагрузки показана на рисунке 1, которая состоит из замкнутой планетарной передачи и дифференциальной планетарной передачи. Бывшие базовые узлы 1c (водило планетарной передачи) и 1s (солнечная шестерня) подключены к узлам 2r (внутреннее кольцо) и 2c (водило планетарной передачи) дифференциальной зубчатой ​​передачи соответственно. Таким образом, разделение нагрузки реализуется за счет входного крутящего момента подшипника шестерни первой и второй ступени одновременно.На рисунке 1 позиции 1r, 1p1, 1s и 1c представляют собой внутреннее кольцо, планетарную шестерню, солнечную шестерню и водило планетарной передачи первой ступени планетарной зубчатой ​​передачи, соответственно, в то время как 2r, 2p1, 2s и 2c представляют соответствующие блоки второй ступени. ступенчатая планетарная передача.


2.2. Скорость каждой единицы планетарной зубчатой ​​передачи первой ступени

Взаимосвязь между скоростью вращения солнечной шестерни, водила планетарной передачи и внутреннего кольца планетарной зубчатой ​​передачи первой ступени показана на

Уравнение (2.2) получается в соответствии с общим соотношением относительного передаточного числа между каждым блоком в принципе планетарной передачи и типом трансмиссии и характеристическим параметром планетарной зубчатой ​​передачи первой ступени:

Мы можем прийти к (3) с помощью (1) и (2.2):

Взаимосвязь между скоростью вращения планетарной шестерни и водилом планетарной передачи и внутренним кольцом выражается как (4) в соответствии с соотношением относительной скорости вращения между каждым блоком в планетарной зубчатой ​​передаче первой ступени: Аналогично (2.2), (5) получается следующим образом:

Таким образом, (6) можно получить, используя (5) и (4): где — характеристический параметр планетарной передачи, а. , и — количество зубьев внутреннего кольца, солнечной шестерни и планетарной шестерни соответственно. и (= c, s, r, p; = c, s, r, p; = c, s, r, p) представляют скорость вращения и относительное передаточное число каждого блока планетарной зубчатой ​​передачи первой ступени, соответственно.

2.3. Скорость каждой единицы планетарной зубчатой ​​передачи второй ступени

Взаимосвязь между скоростью вращения солнечной зубчатой ​​передачи и водила планетарной передачи и внутреннего кольца планетарной зубчатой ​​передачи второй ступени выражается следующим образом:

Уравнение (8) может быть получено по трансмиссионной характеристике базового узла планетарной передачи второй ступени:

Использование (7) и (8) дает

Уравнения (10) и (11) получены из отношения относительного перемещения узлов планетарной зубчатой ​​передачи, когда внутреннее кольцо и водило планетарной передачи второй ступени планетарной зубчатой ​​передачи зафиксированы, соответственно:

Соединяя (10) и (11) с (9), соотношение скорости вращения между входными и выходными блоками планетарной зубчатой ​​передачи второй ступени получается следующим образом:

А соотношение между частотами вращения планетарной передачи выражается следующим образом:

Аналогично (2. 2), (14) можно получить следующим образом:

Замена (14) на (13) дает

Рассматривая схему рисунка 1, (16) можно представить следующим образом:

Подстановка (16) и (3) в (15) дает где — характеристический параметр планетарной линии планетарной передачи второй ступени, а. , и обозначают количество зубьев внутреннего кольца, солнечной шестерни и планетарной шестерни второй планетарной зубчатой ​​передачи, соответственно. — частота вращения каждого блока планетарной зубчатой ​​передачи второй ступени, а (;;) — относительное передаточное число соответствующего блока.

2.4. Передаточное число планетарной зубчатой ​​передачи

Выражения входной и выходной частоты вращения двухступенчатой ​​планетарной зубчатой ​​передачи с разделением нагрузки даются заменой (16) и (3) в (12) следующим образом:

Таким образом, формула передаточного числа двухступенчатой ​​планетарной зубчатой ​​передачи с разделением нагрузки получается как

Общее передаточное число на рисунке 1 связано с характеристическими параметрами планетарных зубчатых передач и. Слишком малые значения и приводят к занижению системы и снижению несущей способности.Значения характеристических параметров должны быть разумными. Рекомендуемый интервал и есть.

Связь между передаточным числом и характеристическими параметрами в двухступенчатой ​​планетарной зубчатой ​​передаче с разделением нагрузки показана на рисунке 2. Передаточное отношение увеличивается с увеличением значений характеристических параметров планетарной зубчатой ​​передачи, а максимальное передаточное число в интервале составляет 73


3. Динамическая модель
3.1. Модель многоступенчатой ​​трансмиссии

Многоступенчатая зубчатая передача, состоящая из двухступенчатой ​​планетарной зубчатой ​​передачи и одноступенчатой ​​зубчатой ​​передачи с параллельными осями, показана на рисунке 3.3g1 и 3g2 на рисунке 3 обозначают ведущую шестерню и ведомую шестерню с параллельными осями.


Динамическая модель на Рисунке 3 показана на Рисунке 4 на основе теории с сосредоточенными параметрами. Поскольку планетарная зубчатая передача первой ступени и планетарная зубчатая передача второй ступени имеют одинаковую базовую конструкцию, они могут быть представлены одноступенчатой ​​чисто крутильной моделью, показанной на рисунке 5.



Линейные перемещения всех элементов системы многоступенчатой ​​передачи показаны следующим образом:

Обобщенные массы всех элементов многоступенчатой ​​системы передачи показаны следующим образом:

3.2. Уравнение динамики многоступенчатой ​​трансмиссии

Сила взаимодействия между солнечной шестерней и планетарной шестерней первой планетарной передачи по линии действия определяется следующим образом:

Сила взаимодействия между внутренним кольцом и планетарной шестерней планетарной передачи первой ступени планетарной передачи по линии действия может быть выражена следующим образом:

Сила взаимодействия между солнечной шестерней и планетарной шестерней планетарной передачи второй ступени по линии действия равна

Сила взаимодействия между внутренним кольцом и планетарной шестерней планетарной передачи второй ступени по линии действия может быть выражена следующим образом:

Сила взаимодействия между ведущей шестерней и ведомой шестерней шестерни третьей ступени с параллельной осью вдоль линии действия может быть выражена следующим образом:

Зафиксируйте внутреннее кольцо планетарной зубчатой ​​передачи первой ступени и примите количество планетарных шестерен планетарной зубчатой ​​передачи равным 3; а именно,. Согласно методам моделирования планетарного механизма в [13], можно построить динамическое уравнение многоступенчатой ​​системы передачи, показанной на рисунке 4, как показано на

Уравнения динамической модели представлены в матричной форме как где вектор смещения, матрица масс, матрица демпфирования, матрица жесткости и вектор нагрузки даны, соответственно, как

4. Характеристика распределения нагрузки многоступенчатой ​​планетарной зубчатой ​​передачи с разделением нагрузки
4.1. Расчет коэффициента распределения нагрузки

Используйте метод численного интегрирования для решения динамического уравнения (28) системы, получите отклики на смещение и скорость системы и подставьте отклики в (22) — (25), и затем получить силы зацепления,, и. Сделать и, соответственно, представляют коэффициенты распределения нагрузки внутреннего и внешнего зацепления всех зубчатых пар планетарной зубчатой ​​передачи первой ступени и как коэффициенты внутреннего и внешнего зацепления всех зубчатых пар планетарной зубчатой ​​передачи второй ступени. ; тогда коэффициенты распределения нагрузки выражаются как где, — номера циклов зацепления для внутреннего и внешнего зацепления планетарной зубчатой ​​пары.

Когда и используются для обозначения коэффициента распределения нагрузки внутреннего и внешнего зацепления каждой шестерни первой ступени и и для каждой шестерни второй ступени в системном периоде, соответственно, выражение может быть представлено следующим образом:

В статье анализируется система передачи, показанная на рисунке 4. Основные параметры системы передачи показаны в таблицах 1 и 2, а другие параметры могут быть определены с помощью [21]. Подставляем соответствующие параметры системы в (28) для решения.Используйте (30) и (31), чтобы получить коэффициенты распределения нагрузки системы передачи.

Параметр Держатель Кольцо Солнечная шестерня Планетарная шестерня
мм 902 210 258
Базовая окружность, (мм) — 682,22 197. 34 242,44
Масса, (кг) 2042,77 410,34 344,91 388,39
Момент инерции, (кг · м 2 ) 462,55 462,55 угол, () — 20 20 20
Радиус шага, (мм) / мм 345550 140 205
Базовый круг, мм — 516.83 131,56 192,64
Масса, (кг) 1212,49 80,56 131,40 176,54
Момент инерции

671		 1,29 5,12
Угол давления, () — 20 20 20

904 ()
Ведущая шестерня Ведомая шестерня
Радиус шага, (мм) 292 100
Базовый круг, (мм) 274. 39 93,97
Масса, (кг) 208,22 24,14
Момент инерции, (кг · м 2 ) 8,87 0,12
20 20
4.2. Влияние ошибки сетки на коэффициент распределения нагрузки системы

На свойство разделения нагрузки планетарной зубчатой ​​передачи в значительной степени влияют производственная ошибка, ошибка установки и ошибка эксцентрика, которыми нельзя пренебречь в планетарной зубчатой ​​передаче.Учитывая сложность системы, предполагается, что эквивалентная погрешность зацепления планетарной передачи каждой ступени в направлении линии зацепления одинакова, и даны значения 10, 20, 30, 40 и 50 мкм м соответственно. Изучаются свойства распределения нагрузки многоступенчатой ​​зубчатой ​​передачи в этих пяти условиях. Взаимосвязи между кривыми коэффициента распределения нагрузки внутреннего и внешнего зацепления первой и второй ступеней, которые рассчитываются согласно (31), показаны на рисунке 6 с различными ошибками сетки.

Результаты, приведенные ниже, можно сделать в соответствии с рисунком 6. (1) Каждый коэффициент распределения нагрузки увеличивается с увеличением ошибки сетки. (2) Коэффициент распределения нагрузки внутреннего зацепления отличается от коэффициента внешнего зацепления при различных ошибках сетки. Максимальные коэффициенты распределения нагрузки с внешним зацеплением и внутренним зацеплением планетарной передачи первой ступени составляют 1,579 и 1,645, соответственно, в то время как коэффициенты распределения нагрузки планетарной передачи второй ступени равны 1,630 и 1,665 соответственно. (3) По сравнению с различиями в скорости изменения Каждый коэффициент распределения нагрузки планетарной передачи второй ступени более очевиден, чем у планетарной передачи первой ступени.Максимальная разница в скорости переключения планетарной передачи первой ступени составляет 0,101 / 50 мкм м, а у планетарной передачи второй ступени — всего 0,003 / 50 мкм м.

4.3. Влияние частоты вращения на коэффициент распределения нагрузки

Для анализа влияния частоты вращения планетарного редуктора первой ступени на коэффициент распределения нагрузки частота вращения устанавливается равной 5 об / мин, 10 об / мин, 15 об / мин, 20 об / мин и 25 об / мин соответственно. Уравнение (31) используется для расчета коэффициента распределения нагрузки в различных условиях, а кривые получены на рисунке 7.

Влияние скорости вращения на коэффициент распределения нагрузки можно сделать ниже, в соответствии с рисунком 7. (1) Каждый коэффициент распределения нагрузки увеличивается с увеличением скорости вращения, что указывает на то, что способность распределения нагрузки планетарной зубчатой ​​передачи ослабляется, а вибрация уменьшается. усугубляется с увеличением скорости вращения. (2) В интервале изменения скорости вращения разница в скорости изменения коэффициента распределения нагрузки между внутренним и внешним зацеплением планетарной зубчатой ​​передачи первой ступени значительно различается; планетарные шестерни первой ступени 1, 2 и 3 равны 1.77%, 0,84% и 1,49% соответственно. Аналогичный результат можно сделать для планетарной зубчатой ​​передачи второй ступени, и вычислены различия в скоростях изменения 1,47%, 2,71% и 2,76% планетарных зубчатых колес 1, 2 и 3 второй ступени, соответственно.

5. Заключение

(1) Динамическая модель построена для учета динамического поведения многоступенчатой ​​планетарной зубчатой ​​передачи, используемой в ветряном генераторе. Модель может служить полезным руководством для динамического проектирования многоступенчатой ​​планетарной зубчатой ​​передачи ветряного генератора.(2) Каждый коэффициент распределения нагрузки планетарной передачи первой ступени изменяется больше, чем у планетарной передачи второй ступени. При той же ошибке сетки коэффициент распределения нагрузки внутренней зацепления второй ступени является наибольшим, коэффициент распределения нагрузки внутренней зацепления первой ступени является вторым по величине, а коэффициент распределения нагрузки внешнего зацепления первой ступени является минимальным ( 3) Распределение нагрузки ослабевает, а вибрация трансмиссии усиливается с увеличением скорости вращения. На каждом интервале частоты вращения коэффициенты распределения нагрузки внутреннего и внешнего зацепления планетарной зубчатой ​​передачи второй ступени изменяются сильнее, чем коэффициенты планетарной зубчатой ​​передачи первой ступени.

Номенклатура
: Угловое смещение элемента (,,;, 2, 3)
: Радиусы основания шестерни,;
: Радиус круга, проходящего через центры планет
: Радиусы -й ступени круга, проходящего через центры планет;
: Угол зацепления планетарной передачи
: Угол зацепления кольцевой планетарной передачи
: Общее количество комплектов планетарных передач для трансмиссии третьей ступени;
: Момент инерции полярной массы элемента трансмиссии 1-й ступени;
: Масса планетарной шестерни 1-й ступени
: =
: Момент инерции полярной массы элемента трансмиссии 2-й ступени;
: Масса планетарной шестерни 2-й ступени
: =
: Радиусы основания шестерни шестерни трансмиссии третьей ступени; ;
: Угол зацепления солнечная планета трансмиссии ступени th;
: Угол зацепления кольцевой планетарной передачи трансмиссии ступени th;
: Ошибка сетки Солнце-планета
: Ошибка сетки Кольцо-Планета
: Жесткость сетки Солнце-Планета
:
: жесткость Кольцо-Планета
: Коэффициент демпфирования сетки Солнце-Планета
: Коэффициент демпфирования сетки Кольцо-Планета
: Угловое смещение ступени трансмиссии трансмиссии th; ; ;
: Ошибка зацепления солнечной планетарной передачи планетарной передачи th для привода ступени th; ;
: Ошибка зацепления кольцевой планетарной передачи планетарной передачи -й планетарной передачи для трансмиссии th-ступени; ;
: Погрешность зацепления шестерен с параллельными валами
: Жесткость зацепления солнечной планетарной передачи планетарной шестерни th для привода ступени th; ;
: Жесткость зацепления планетарного кольца планетарной передачи -й планетарной передачи для трансмиссии -й ступени; ;
: Жесткость зацепления шестерен с параллельными валами
: Жесткость на кручение, связанная с солнцем 1-й ступени и водилом 2-й ступени
: Жесткость на кручение и связанная с водилом 1-й ступени Кольцо 2-й ступени
: Жесткость на кручение, связанная с солнечной шестерней 2-й ступени и шестерней 3-й ступени
: Коэффициент демпфирования зацепления солнечно-планетарной зацепления планетарной шестерни th для привода трансмиссии th; ;
: Коэффициент демпфирования зацепления кольцевой планетарной передачи планетарной передачи th для привода ступени th; ;
Коэффициент демпфирования зацепления шестерен с параллельными валами
: Коэффициент демпфирования крутильных колебаний, связанный с солнцем 1-й ступени и водилом 2-й ступени
: Коэффициент демпфирования крутильных колебаний 1-й-й ступени водило и кольцо 2-й ступени
: Коэффициент демпфирования крутильных колебаний, связанный с солнцем 2-й ступени и шестерней 3-й ступени
: Входной крутящий момент
: Выходной крутящий момент.
Конфликт интересов

Авторы заявляют, что у них нет конфликта интересов в отношении публикации этой статьи.

Благодарности

Авторы выражают признательность за поддержку Китайскому национальному научному фонду (№ 51175299), Фонду естественных наук провинции Шаньдун, Китай (№ ZR2010EM012), Независимому инновационному фонду Университета Шаньдун (IIFSDU2012TS044) и Выпускник Независимого инновационного фонда Шаньдунского университета, ГИИФСДУ (№yzc10117).

Анализ динамического поведения многоступенчатой ​​планетарной зубчатой ​​передачи, используемой в ветроэнергетическом генераторе

3.1. Модель многоступенчатой ​​трансмиссии

На рисунке показана многоступенчатая зубчатая передача, состоящая из двухступенчатой ​​планетарной зубчатой ​​передачи и одноступенчатой ​​зубчатой ​​передачи с параллельными осями. 3g1 и 3g2 в стойке для ведущей шестерни и ведомой шестерни параллельной оси.

Система трансмиссии многоступенчатой ​​планетарной передачи с разделением нагрузки.

Показана динамическая модель, основанная на теории сосредоточенных параметров.Поскольку планетарная зубчатая передача первой ступени и планетарная зубчатая передача второй ступени имеют одинаковую базовую конструкцию, они могут быть представлены одноступенчатой ​​чисто крутильной моделью, показанной на рис.

Динамическая модель многоступенчатой ​​планетарной передачи с разделением нагрузки.

Торсионная модель одноступенчатой ​​планетарной передачи.

Линейные перемещения всех элементов многоступенчатой ​​системы передачи показаны следующим образом:

u1c = r1cθ1c, u2c = r2cθ2c, u1s = r1bsθ1s, u2s = r2bsθ2s, u1r = r1brθ1r, u2r = r2brθ2r, u1pj = r1bpjθ1pj, u1pj = r1bpjθ1pj, u2pjθ1 = u2pj2 = u2pj3g2 = r2gθ3g2 = rpj3g2 = r2gθ3g2 = rpj3g3g2 = rpj3g2g3g2 = rpj3g2g3g2g3g2g2g2g2g3g2g3g2g3g2g3g2g3g2g3g2g3g2g2g2g2g2g3g2g2g2

(20)

Обобщенные массы всех элементов многоступенчатой ​​системы передачи показаны следующим образом:

m1c = I1cer1c2, m2c = I2cer2c2, m1s = I1sr1bs2, m2s = I2sr2bs2, m1r = I1rr1br2, m2r = I2rr2br2, m1pj = I1pjr1bpj2, m2pj3g2 = I2pj2g = I2pjg2, m3j3g2g, m3jg2g2 = I2pjg2 = I2pj2

(21)

3.2. Уравнение динамики многоступенчатой ​​трансмиссии

Сила взаимодействия между солнечной шестерней и планетарной шестерней j -й планетарной передачи первой ступени планетарной передачи по линии действия определяется следующим образом:

F1spj = K1spjX1spj + C1spjX˙1spj, X1spj = u1s + u1pj − cosα1su1c − E1spj, X˙1spj = u˙1s + u˙1pj − cosα1su˙1c − E˙1spj.

(22)

Сила взаимодействия между внутренним кольцом и планетарной шестерней j -й планетарной передачи первой ступени по линии действия может быть выражена следующим образом:

F1rpj = K1rpjX1rpj + C1rpjX˙1rpj, X1rpj = u1pj − u1r + cosα1ru1c − E1rpj, X˙1rpj = u˙1pj − u˙1r + cosα1ru˙1c − E˙1rpj.

(23)

Сила взаимодействия между солнечной шестерней и j -й планетарной шестерней планетарной зубчатой ​​передачи второй ступени по линии действия равна

F2spj = K2spjX2spj + C2spjX˙2spj, X2spj = u2s + u2pj − cosα2su2c − E2spj, X˙2spj = u˙2s + u˙2pj − cosα2su˙2c − E˙2spj.

(24)

Сила взаимодействия между внутренним кольцом и планетарной шестерней j -й планетарной передачи второй ступени планетарной передачи по линии действия может быть выражена следующим образом:

F2rpj = K2rpjX2rpj + C2rpjX˙2rpj, X2rpj = u2pj − u2r + cosα2ru2c − E2rpj, X˙2rpj = u˙2pj − u˙2r + cosα2ru˙2c − E˙2rpj.

(25)

Сила взаимодействия между ведущей шестерней и ведомой шестерней шестерни третьей ступени с параллельной осью вдоль линии действия может быть выражена следующим образом:

F3g1g2 = K3g1g2X3g1g2 + C3g1g2X˙3g1g2, X3g1g2 = u3g1 + u3g2 − E3g1g2, X˙3g1g2 = u˙3g1 + u˙3g2 − E˙3g1g2.

(26)

Зафиксируйте внутреннее кольцо планетарной зубчатой ​​передачи первой ступени и примите количество планетарных шестерен планетарной зубчатой ​​передачи равным 3; а именно, 1 N = 2 N = 3. Согласно методам моделирования планетарного механизма в [13], можно построить динамическое уравнение многоступенчатой ​​системы передачи, показанной на рисунке, как показано на

m1cu¨1c − cosα1s∑j = 11NF1spj + cosα1r∑j = 11NF1rpj + K1c2rr1c (u1cr1c − u2rr2br) + C1c2rr1c (u˙1cr1c − u˙2rr2bs (u˙1cr1c − u˙2rr2bs) = Tir1cr1 + msr1 + m1 + m1 + m1 + m1 + 1 + m u2cr2c) + C1s2cr1bs (u˙1sr1bs-u˙2cr2c) = 0, m1p1u¨1p1 + F1sp1 + F1rp1 = 0, m1p2u¨1p2 + F1sp2 + F1rp2 = 0, ⋮ m1p1Nu¨1p1N + m2rpsp1N + m2rpsp1N + −cosα2s∑j = 12NF2spj + cosα2r∑j = 12NF2rpj −K1s2cr2c (u1sr1bs − u2cr2c) −C1s2cr2c (u˙1sr1bs − u˙2cr2c) = 0, m2su¨2s + ∑bj3gr2s () u˙2sr2bs − u˙3g1r3bg1) = 0, m2p1u¨2p1 + F2sp1 + F2rp1 = 0, m2p2u¨2p2 + F2sp2 + F2rp2 = 0, ⋮ m2p2Nu¨2p2N + F2sp2N + F2rp2N2 = −2 rp2N = 0, r2rpjn = 0, r2rp2n = 0, r2 -K1c2rr2br (u1cr1c-u2rr2br) -C1c2rr2br (u˙1cr1c-u˙2rr2br) = 0, m3g1u¨3g1 + F3g1g2-K2s3g1r3bg1 (u2sr2bs-u3g1r3bg1) -C2s3g1r3bg1 (u˙2sr2bs-u˙3g1r3bg1) = 0, m3g2u¨3g2 + F3g1g2 + Tor3bg2 = 0.

(27)

Уравнения динамической модели представлены в матричной форме как

где вектор смещения, матрица масс, матрица демпфирования, матрица жесткости и вектор нагрузки задаются, соответственно, как

u = [u1c, u1s, u1p1, u1p2, u1p3, u2c, u2s, u2p1, u2p2, u2p3, u2r, u3g1, u3g2] T, M = diag (m1c, m1s, m1p1, m1p2, m1p3, m2c, m2s, m2p1, m2p2, m2p3, m2r, m3g1, m3g2), C = [C1c2rr1c2 + cosα1s2 13C1spj + cosα1r2Σj = 13C1rpj-cosα1sΣj = 13C1spjC1rp1cosα1r-C1sp1cosα1sC1rp2cosα1r-C1sp2cosα1s ⋯ -cosα1sΣj = 13C1spjC1s2cr1bs2 + Σj = 13C1spjC1sp1 ⋯ C1sp1 + C1rp10 ⋯ C1sp2 + C1rp2 ⋯ symmetric⋱], K = [K1c2rr1c2 + cosα1s2Σj = 13K1spj + cosα1r2Σj = 13K1rpj-cosα1sΣj = 13K1spjK1rp1cosα1r-K1sp1cosα1sK1rp2cosα1r-K1sp2cosα1s ⋯ -cosα1sΣj = 13K1spjK1s2cr1bs2 + Σj = 13K1spjK1sp1 ⋯ K1sp1 + K1rp10 ⋯ K1sp2 + K1rp2 ⋯ symmetric⋱], F = [Tir1c-cosα1s (Σj = 13C1spjE˙1spj + Σj = 13K1spjE1spj) + cosα1r (Σj = 13C1rpjE˙1rpj + Σj = 13K1rpjE1rpj) Σj = 13C1spjE˙1spj + Σj = 13K1spjE1spjC1sp1E˙1sp1 + K1sp1E1sp1 + C1rp1E˙1rp1 + K1rp1E1rp1C1sp2E˙1sp2 + K1sp2E1sp2 + C1rp2E˙ 1rp2 + K1rp2E1rp2C1sp3E˙1sp3 + K1sp3E1sp3 + C1rp3E˙1rp3 + K1rp3E1rp3cosα2r (∑j = 13K2rpjE2rpj + ∑j = 13C2rpjE˙2rpj2 = 13C2rpjE˙2rpj2 spj2 + spj2 + cos − jE˙2spj) ⋮].

(29)

Индекс